题目内容
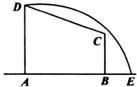 如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=| 3 |
(1)建立适当的直角坐标系,求曲线段DE的方程;
(2)过C能否作一条直线与曲线段DE相交,且所得弦以C为中点,如果能,求该弦所在的直线的方程;若不能,说明理由.
分析:(!)由题意,先建立平面直角坐标系,利用曲线的方程这一概念求其动点的轨迹方程,要注意求解方程之后要有题意去排杂;
(2)对于(2)这种是否C能否,往往要利用假设的思想,设出变量,存在建立方程求解,不存在会产生矛盾及可求解.
(2)对于(2)这种是否C能否,往往要利用假设的思想,设出变量,存在建立方程求解,不存在会产生矛盾及可求解.
解答:解:(1)以直线AB为x轴,线段AB的中点为原点建立直角坐标系,
则A(-2,0),B(2,0),C(2,
),D(-2,3).
依题意,曲线段DE是以A、B为焦点的椭圆的一部分.
∵a=
(|AD|+|BD|)=4,c=2,b2=12,
∴所求方程为
+
=1(-2≤x≤4,0≤y≤2
).
(2)设这样的弦存在,其方程y-
=k(x-2),即y=k(x-2)+
,将其代入
+
=1
得(3+4k2)x2+(8
k-16k2)x+16k2-16
k-36=0
设弦的端点为M(x1,y1),N(x2,y2),则由
=2,知x1+x2=4,∴-
=4,解得k=-
.
∴弦MN所在直线方程为y=-
x+2
,验证得知,这时M(0,2
),N(4,0)适合条件.
故这样的直线存在,其方程为y=-
x+2
.
则A(-2,0),B(2,0),C(2,
| 3 |
依题意,曲线段DE是以A、B为焦点的椭圆的一部分.
∵a=
| 1 |
| 2 |
∴所求方程为
| x2 |
| 16 |
| y2 |
| 12 |
| 3 |
(2)设这样的弦存在,其方程y-
| 3 |
| 3 |
| x2 |
| 16 |
| y2 |
| 12 |
得(3+4k2)x2+(8
| 3 |
| 3 |
设弦的端点为M(x1,y1),N(x2,y2),则由
| x1+x2 |
| 2 |
8
| ||
| 3+4k2 |
| ||
| 2 |
∴弦MN所在直线方程为y=-
| ||
| 2 |
| 3 |
| 3 |
故这样的直线存在,其方程为y=-
| ||
| 2 |
| 3 |
点评:(1)重点考查了利用曲线的方程这一概念,先建立平面直角坐标系,然后利用定义法求其动点的轨迹方程,并进行实际问题的排杂;
(2)重点考查了假设存在,建立方程求解或找矛盾的这一常用方法,还考查了直线方程与曲线方程产生交点要联立,用设而不求整体代换的思想求解.
(2)重点考查了假设存在,建立方程求解或找矛盾的这一常用方法,还考查了直线方程与曲线方程产生交点要联立,用设而不求整体代换的思想求解.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 如图所示,在直角梯形OABC中,
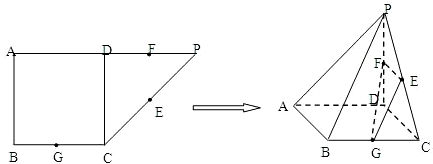
如图所示,在直角梯形OABC中,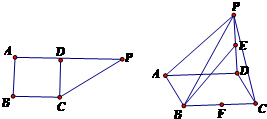 如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.
如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.