题目内容
如图所示,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=| 1 | 2 |
(1)求证:AP∥平面EFG;
(2)求二面角G-EF-D的大小.
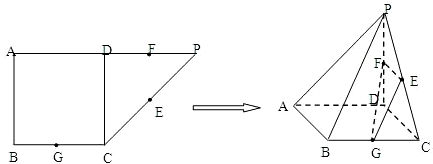
分析:(1)由题意及图形,抓住折叠前与折叠后之间的连系,利用条件在平面内找到与直线平行的直线用线面平行的判定定理进行证明.
(2)由题意及(1)可以知道利用二面角的概念找到二面角的平面角,然后再三角形中解出二面角的大小.
(2)由题意及(1)可以知道利用二面角的概念找到二面角的平面角,然后再三角形中解出二面角的大小.
解答: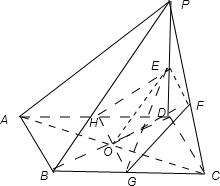 解:由题意画出如下图形:
解:由题意画出如下图形:
(1)连接AC,BD交与点O,连接GO,FO,EO,
∵E,F分别为PC,PD的中点,
∴EF
CD ,GO
CD∴EF
GO
∴四边形EFOG是平行四边行,∴EO?平面EFOG,又在△PAC中,
E,O分别为PC,AC的中点∴PA∥EOEO?平面EFOGPA不在平面EFOG
∴PA∥平面EFOG,即PA∥平面EFG;
(2)取AD的中点H,连接GH,则由GH∥CD∥EF知平面EFG即为平面EFGH,
由已知底面ABCD为正方形∴AD⊥DC
又∵PD⊥平面ABCD∴PD⊥CD又PD∩DC=D∴CD⊥平面PAD
又EF∥CD∴EF⊥平面PAD∴EF⊥FD,EF⊥FH∴∠HFD为二面角的平面角
在直角三角形FDH中,由FD=DH=1得∠HFD=45°,故二面角G-EF-D的平面角为45°.
 解:由题意画出如下图形:
解:由题意画出如下图形:(1)连接AC,BD交与点O,连接GO,FO,EO,
∵E,F分别为PC,PD的中点,
∴EF
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
∴四边形EFOG是平行四边行,∴EO?平面EFOG,又在△PAC中,
E,O分别为PC,AC的中点∴PA∥EOEO?平面EFOGPA不在平面EFOG
∴PA∥平面EFOG,即PA∥平面EFG;
(2)取AD的中点H,连接GH,则由GH∥CD∥EF知平面EFG即为平面EFGH,
由已知底面ABCD为正方形∴AD⊥DC
又∵PD⊥平面ABCD∴PD⊥CD又PD∩DC=D∴CD⊥平面PAD
又EF∥CD∴EF⊥平面PAD∴EF⊥FD,EF⊥FH∴∠HFD为二面角的平面角
在直角三角形FDH中,由FD=DH=1得∠HFD=45°,故二面角G-EF-D的平面角为45°.
点评:此题重点考查了学生们的空间想象能力,还考查了正方形的特点及折叠前后之间的不变量及线面平行的判定定理,此外还考查了利用二面角平面角的定义在三角形中求解二面角的大小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
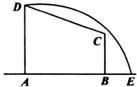 如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|= 如图所示,在直角梯形OABC中,
如图所示,在直角梯形OABC中,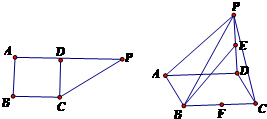 如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.
如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.