题目内容
(2013•徐州模拟)设中心在原点的双曲线与椭圆
+y2=1有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程是
| x2 | 2 |
2x2-2y2=1
2x2-2y2=1
.分析:欲求双曲线方程,只需求出双曲线中的a,b的值即可,根据双曲线与椭圆
+y2=1有公共的焦点,求出椭圆中的c值,也即双曲线中的c值,再求出椭圆中的离心率,因为椭圆与双曲线的离心率互为倒数,所以可得双曲线中离心率,据此求出a值,再利用a,b,c之间的关系式,就可得到双曲线的方程.
| x2 |
| 2 |
解答:解:椭圆
+y2=1中c=1
∵中心在原点的双曲线与椭圆
+y2=1有公共的焦点
∴双曲线中c=1,
∵椭圆
+y2=1的离心率为
=
,椭圆与双曲线的离心率互为倒数.
∴双曲线的离心率为
,
∴双曲线中a=
,b2=c2-a2=
,b=
∴双曲线的方程为2x2-2y2=1
故答案为2x2-2y2=1.
| x2 |
| 2 |
∵中心在原点的双曲线与椭圆
| x2 |
| 2 |
∴双曲线中c=1,
∵椭圆
| x2 |
| 2 |
| c |
| a |
| ||
| 2 |
∴双曲线的离心率为
| 2 |
∴双曲线中a=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴双曲线的方程为2x2-2y2=1
故答案为2x2-2y2=1.
点评:本题主要考查了椭圆,双曲线的标准方程以及性质的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
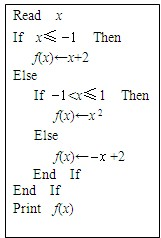 (2013•徐州模拟)已知某算法的伪代码如图,根据伪代码,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是
(2013•徐州模拟)已知某算法的伪代码如图,根据伪代码,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是