题目内容
12.直线l1与l2是圆x2+y2=1的两条切线,若l1与l2的交点为(1,2),则l1与l2的夹角的正切值等于$\frac{4}{3}$.分析 作出对应的图象,设∠OBA=θ,求出tanθ,利用正切的倍角公式进行求解即可.
解答 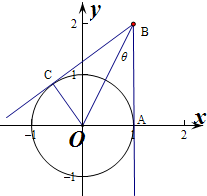 解:作出对应的图象如图:
解:作出对应的图象如图:
则B(1,2),A(1,0),
设∠OBA=θ,
则tanθ=$\frac{OA}{AB}=\frac{1}{2}$,
则l1与l2的夹角为∠ABC=2θ,
则tan∠ABC=tan2θ=$\frac{2tanθ}{1-ta{n}^{2}θ}$=$\frac{2×\frac{1}{2}}{1-(\frac{1}{2})^{2}}=\frac{1}{1-\frac{1}{4}}$=$\frac{4}{3}$,
故答案为:$\frac{4}{3}$
点评 本题主要考查三角函数值的求解,根据直线和圆相切的位置关系,求出tanθ,利用正切的倍角公式是解决本题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
3.已知各项均为正数的等比数列{an}中,3a1,$\frac{1}{2}$a3,2a2成等差数列,则$\frac{{a}_{11}+{a}_{13}}{{a}_{8}+{a}_{10}}$=( )
| A. | 27 | B. | 3 | C. | -1或3 | D. | 1或27 |
1.用均匀随机数进行随机模拟,可以解决( )
| A. | 只能求几何概型的概率,不能解决其他问题 | |
| B. | 不仅能求几何概型的概率,还能计算图形的面积 | |
| C. | 不但能估计几何概型的概率,还能估计图形的面积 | |
| D. | 最适合估计古典概型的概率 |