题目内容
1.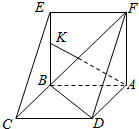 如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.
如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.(1)若∠CBE=120°,求三棱锥B-ADF的外接球的表面积;
(2)若K为线段BE上异于B,E的点,CE=2$\sqrt{2}$.设直线AK与平面BDF所成角为φ,当30°≤φ≤45°时,求BK的取值范围.
分析 (1)求出外接球的半径,利用取得面积公式求解即可.
(2)证明BE⊥平面ABCD.=以B为原点,BC、BA、BE的方向分别为x轴、y轴、z轴的正方向,求出相关点的坐标,求出平面BDF的一个法向量为$\overrightarrow{n}$=(x,y,z).推出sinφ=$\left|\frac{\overrightarrow{n}•\overrightarrow{AK}}{\left|\overrightarrow{n}\right|•\left|\overrightarrow{AK}\right|}\right|$=$\frac{|2+m|}{\sqrt{3}•\sqrt{4+{m}^{2}}}$,结合$\frac{1}{2}≤$sinφ$≤\frac{\sqrt{2}}{2}$,即求出BK的取值范围.
解答 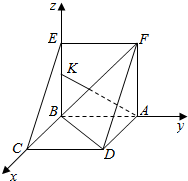 解:(1)三棱锥B-ADF的外接球就是三棱柱DFA-CEB的外接球,球的半径为R,R=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
解:(1)三棱锥B-ADF的外接球就是三棱柱DFA-CEB的外接球,球的半径为R,R=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
外接球的表面积为:4πR2=20π.
(2)解:∵BE=BC=2,CE=2$\sqrt{2}$,∴CE2=BC2+BE2,
∴△BCE为直角三角形,BE⊥BC,…(2分)
又BE⊥BA,BC∩BA=B,BC、BA?平面ABCD,
∴BE⊥平面ABCD. …(6分)
以B为原点,BC、BA、BE的方向分别
为x轴、y轴、z轴的正方向,
建立空间直角坐标系,则B(0,0,0),F(0,2,2),A(0,2,0),$\overrightarrow{BD}$=(2,2,0),$\overrightarrow{BF}=(0,2,2)$.
设K(0,0,m),平面BDF的一个法向量为$\overrightarrow{n}$=(x,y,z).
由$\overrightarrow{n}•\overrightarrow{BD}=0$,$\overrightarrow{n}•\overrightarrow{BF}=0$,得$\left\{\begin{array}{l}2x+2y=0\\ 2y+2z=0\end{array}\right.$,可取$\overrightarrow{n}=(1,-1,0)$,…(10分)
又$\overrightarrow{AK}$=(0,-2,m),于是sinφ=$\left|\frac{\overrightarrow{n}•\overrightarrow{AK}}{\left|\overrightarrow{n}\right|•\left|\overrightarrow{AK}\right|}\right|$=$\frac{|2+m|}{\sqrt{3}•\sqrt{4+{m}^{2}}}$,
∵30°≤φ≤45°,∴$\frac{1}{2}≤$sinφ$≤\frac{\sqrt{2}}{2}$,即$\left\{\begin{array}{l}\frac{1}{2}≤\frac{|2+m|}{\sqrt{3}•\sqrt{4+{m}^{2}}}\\ \frac{|2+m|}{\sqrt{3}•\sqrt{4+{m}^{2}}}≤\frac{\sqrt{2}}{2}\end{array}\right.$…(11分)
结合0<m<2,解得$0<m≤4-2\sqrt{3}$,即BK的取值范围为(0,$4-2\sqrt{3}$].…(12分)
点评 本题考查几何体的外接球的表面积的求法,直线与平面所成角的求法与应用,考查空间想象能力以及计算能力,

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| A. | 3 | B. | -1 | C. | $1+2\sqrt{3}$ | D. | $1-2\sqrt{3}$ |
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
| A. | f(3)<f(1)<f(2) | B. | f(1)<f(2)<f(3) | C. | f(2)<f(1)<f(3) | D. | f(3)<f(2)<f(1) |
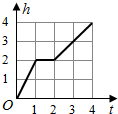
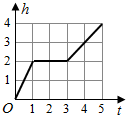
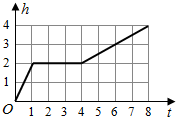
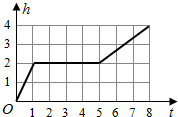
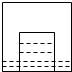 一天,小亮看到家中的塑料桶中有一个竖直放置的玻璃杯,桶子和玻璃杯的形状都是圆柱形,桶口的半径是杯口半径的2倍,其主视图如左图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h与注水时间t之间关系的大致图象是( )
一天,小亮看到家中的塑料桶中有一个竖直放置的玻璃杯,桶子和玻璃杯的形状都是圆柱形,桶口的半径是杯口半径的2倍,其主视图如左图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h与注水时间t之间关系的大致图象是( )