题目内容
13.在△ABC中,已知$\overrightarrow{|AB|}=\sqrt{3},\overrightarrow{|AC}|=\overrightarrow{|BC|}=1$,则 $\overrightarrow{AB}•\overrightarrow{AC}$=$\frac{3}{2}$.分析 如图所示,$\overrightarrow{|AB|}=\sqrt{3},\overrightarrow{|AC}|=\overrightarrow{|BC|}=1$,取AB的中点D,连接CD,则CD⊥AB.在Rt△ACD中,可得cosA=$\frac{AD}{AC}$=$\frac{\sqrt{3}}{2}$,再利用数量积运算性质即可得出.
解答 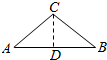 解:如图所示,
解:如图所示,
∵$\overrightarrow{|AB|}=\sqrt{3},\overrightarrow{|AC}|=\overrightarrow{|BC|}=1$,
取AB的中点D,连接CD,则CD⊥AB.
在Rt△ACD中,cosA=$\frac{AD}{AC}$=$\frac{\sqrt{3}}{2}$,
∴A=30°.
∴$\overrightarrow{AB}•\overrightarrow{AC}$=$\sqrt{3}×1×cos3{0}^{°}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了等腰三角形的性质、数量积运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
3.已知α是三角形的内角,sin(α+$\frac{π}{3}$)=$\frac{4}{5}$,则cos($\frac{5π}{12}$-α)=( )
| A. | $\frac{\sqrt{2}}{10}$ | B. | -$\frac{\sqrt{2}}{10}$ | C. | -$\frac{7\sqrt{2}}{10}$ | D. | $\frac{7\sqrt{2}}{10}$ |
4.给出如下命题,正确的序号是( )
| A. | 命题:?x∈R,x2≠x的否定是:?x0∈R,使得x02≠x | |
| B. | 命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5 | |
| C. | 若ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件 | |
| D. | 命题:?x0∈R,x02+a<0为假命题,则实数a的取值范围是a>0 |
8.若函数y=x2+ax+3为偶函数,则a=( )
| A. | 2 | B. | 1 | C. | -1 | D. | 0 |
2.在等比数列{an}中,a1=3,a3=12,则a5=( )
| A. | 48 | B. | -48 | C. | ±48 | D. | 36 |
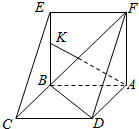 如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.
如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.