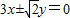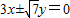题目内容
若F1,F2是双曲线
-
=1(a>0,b>0)与椭圆
+
=1的共同的左、右焦点,点P是两曲线的一个交点,且△PF1F2为等腰三角形,则该双曲线的渐近线方程是 .
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 25 |
| y2 |
| 9 |
分析:先根据两曲线的焦点相同,得双曲线中参数a、b间的一个等式,再利用椭圆的定义,在椭圆中计算两个焦半径PF1、PF2,再利用双曲线的定义,即可得双曲线的a值,从而确定双曲线的标准方程,进而求其渐近线方程.
解答:解:∵椭圆
+
=1的焦点坐标为(±4,0),
∴双曲线
-
=1(a>0,b>0)中c=4,a2-b2=16 ①
设P为两曲线在第一象限的交点,
则在椭圆中,△PF1F2为等腰三角形,
∴PF1=F1F2=8,∴PF2=10-8=2
在双曲线中,2a=PF1-PF2=6,∴a=3 ②
由①②得,双曲线中a=3,b=
,
∴该双曲线的渐近线方程是y=±
x.
故答案为:y=±
x.
| x2 |
| 25 |
| y2 |
| 9 |
∴双曲线
| x2 |
| a2 |
| y2 |
| b2 |
设P为两曲线在第一象限的交点,
则在椭圆中,△PF1F2为等腰三角形,
∴PF1=F1F2=8,∴PF2=10-8=2
在双曲线中,2a=PF1-PF2=6,∴a=3 ②
由①②得,双曲线中a=3,b=
| 7 |
∴该双曲线的渐近线方程是y=±
| ||
| 3 |
故答案为:y=±
| ||
| 3 |
点评:本题主要考查了椭圆和双曲线的定义及其标准方程,椭圆和双曲线的几何性质的综合运用,恰当的在两曲线中研究点P的特点是解决本题的关键.

练习册系列答案
相关题目
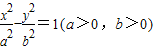 与椭圆
与椭圆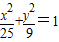 的共同焦点,点P是两曲线的一个交点,且△PF1F2为等腰三角形,则该双曲线的渐近线方程是( )
的共同焦点,点P是两曲线的一个交点,且△PF1F2为等腰三角形,则该双曲线的渐近线方程是( )