��Ŀ����
��֪����f��x��=x3+ax2+bx+c���ڶ�����x��[-2��2]�ϱ�ʾ�����߹�ԭ�㣬����x=±1��������б�ʾ�Ϊ-1�����������⣺��f��x�����溯��������f��x����[s��t]�ڵݼ�����|t-s|�����ֵΪ4����f��x�������ֵΪM����СֵΪm����M+m=0��������?x��[-2��2]��k��f'��x�����������k�����ֵΪ2��������ȷ����ĸ����У� ��A��1��
B��2��
C��3��
D��4��
���𰸡��������������õ����ļ������弰����f��x����ԭ�㣬�з��������f��x���Ľ���ʽ��Ȼ������溯���Ķ����жϺ���f��x������ż�ԣ�����f�䣨x������Сֵ���k�����ֵ��������٢ܵó��жϣ������f�䣨x��=0�����f��x���ļ�ֵ�㣬�������f��x���ĵ�����������ֵ��������ڢ۵ó��жϣ�
����⣺����f��x��=x3+ax2+bx+c��ͼ���ԭ�㣬�ɵ�c=0��
��f�䣨x��=3x2+2ax+b����f��x����x=±1��������б�ʾ�Ϊ-1��
����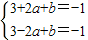 �����a=0��b=-4��
�����a=0��b=-4��
����f��x��=x3-4x��f�䣨x��=3x2-4��
�ٿɼ�f��x��=x3-4x���溯������ˢ���ȷ��
x��[-2��2]ʱ��[f�䣨x��]min=-4����k��f'��x�����������k��-4����ˢܴ���
����f�䣨x��=0����x=±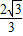 ��
��
����f��x����[-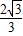 ��
��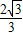 ]�ڵݼ�����|t-s|�����ֵΪ
]�ڵݼ�����|t-s|�����ֵΪ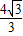 ����ˢڴ���
����ˢڴ���
��f��x���ļ���ֵΪf��-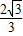 ��=
��=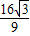 ����СֵΪf��
����СֵΪf��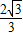 ��=-
��=-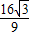 �����˵㴦f��-2��=f��2��=0��
�����˵㴦f��-2��=f��2��=0��
����f��x�������ֵΪM=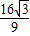 ����СֵΪm=-
����СֵΪm=-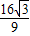 ����M+m=0����ˢ���ȷ��
����M+m=0����ˢ���ȷ��
��ѡB��
������������Ҫ���鵼���ļ������弰���õ����о����������ԡ���ֵ�ķ�����
����⣺����f��x��=x3+ax2+bx+c��ͼ���ԭ�㣬�ɵ�c=0��
��f�䣨x��=3x2+2ax+b����f��x����x=±1��������б�ʾ�Ϊ-1��
����
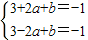 �����a=0��b=-4��
�����a=0��b=-4������f��x��=x3-4x��f�䣨x��=3x2-4��
�ٿɼ�f��x��=x3-4x���溯������ˢ���ȷ��
x��[-2��2]ʱ��[f�䣨x��]min=-4����k��f'��x�����������k��-4����ˢܴ���
����f�䣨x��=0����x=±
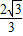 ��
������f��x����[-
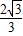 ��
��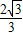 ]�ڵݼ�����|t-s|�����ֵΪ
]�ڵݼ�����|t-s|�����ֵΪ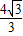 ����ˢڴ���
����ˢڴ�����f��x���ļ���ֵΪf��-
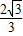 ��=
��=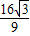 ����СֵΪf��
����СֵΪf��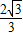 ��=-
��=-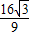 �����˵㴦f��-2��=f��2��=0��
�����˵㴦f��-2��=f��2��=0������f��x�������ֵΪM=
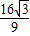 ����СֵΪm=-
����СֵΪm=-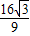 ����M+m=0����ˢ���ȷ��
����M+m=0����ˢ���ȷ����ѡB��
������������Ҫ���鵼���ļ������弰���õ����о����������ԡ���ֵ�ķ�����

��ϰ��ϵ�д�
�����Ŀ
 ��֪����f��x��=Asin����x+�գ���x��R��A��0���أ�0��|��|��
��֪����f��x��=Asin����x+�գ���x��R��A��0���أ�0��|��|��| �� |
| 2 |
A��f(x)=2sin(��x+
| ||
B��f(x)=2sin(2��x+
| ||
C��f(x)=2sin(��x+
| ||
D��f(x)=2sin(2��x+
|