题目内容
已知数列{an}的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列{an} 前n项和为Sn,且满足S3=a4,a3+a5=2+a4
(1)求数列{an}的通项公式;
(2)求数列{an}前2k项和S2k;
(3)在数列{an}中,是否存在连续的三项am,am+1,am+2,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数m的值;若不存在,说明理由.
(1)求数列{an}的通项公式;
(2)求数列{an}前2k项和S2k;
(3)在数列{an}中,是否存在连续的三项am,am+1,am+2,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数m的值;若不存在,说明理由.
分析:(1)等差数列和等比数列的通项公式即可得出;
(2)利用等差数列的通项公式即可得出;
(3)在数列{an}中,仅存在连续的三项a1,a2,a3,按原来的顺序成等差数列,此时正整数m的值为1.分类讨论am=a2k,am=a2k-1,证明不成立即可.
(2)利用等差数列的通项公式即可得出;
(3)在数列{an}中,仅存在连续的三项a1,a2,a3,按原来的顺序成等差数列,此时正整数m的值为1.分类讨论am=a2k,am=a2k-1,证明不成立即可.
解答:解:(1)设等差数列的公差为d,等比数列的公比为q,
则a1=1,a2=2,a3=1+d,a4=2q,a5=1+2d.
∵S3=a4,∴1+2(1+d)=2q,即4+d=2q,
又a3+a5=2+a4,∴1+d+1+2d=2+2q,即3d=2q,解得d=2,q=3.
∴对于k∈N*,有a2k-1=1+(k-1)•2=2k-1,
故an=
,k∈N*.
(2)S2k=(a1+a3+…+a2k-1)+(a2+a4+…+a2k)=[1+3+…+(2k-1)]+2(1+3+32+…+3k-1)=
+
=k2-1+3k.
(3)在数列{an}中,仅存在连续的三项a1,a2,a3,按原来的顺序成等差数列,此时正整数m的值为1,下面说明理由
若am=a2k,则由am+am+2=2am+1,得2×3k-1+2×3k=2(2k+1).
化简得4•3k-1=2k+1,此式左边为偶数,右边为奇数,不可能成立.
若am=a2k-1,则由am+am+2=2am+1,得(2k-1)+(2k+1)=2×2×3k-1
化简得k=3k-1,
令Tk=
(k∈N*),则Tk+1-Tk=
-
=
<0.
因此,1=T1>T2>T3>…,故只有T1=1,此时K=1,m=2×1-1=1.
综上,在数列{an}中,仅存在连续的三项a1,a2,a3,按原来的顺序成等差数列,此时正整数m的值为1.
则a1=1,a2=2,a3=1+d,a4=2q,a5=1+2d.
∵S3=a4,∴1+2(1+d)=2q,即4+d=2q,
又a3+a5=2+a4,∴1+d+1+2d=2+2q,即3d=2q,解得d=2,q=3.
∴对于k∈N*,有a2k-1=1+(k-1)•2=2k-1,
故an=
|
(2)S2k=(a1+a3+…+a2k-1)+(a2+a4+…+a2k)=[1+3+…+(2k-1)]+2(1+3+32+…+3k-1)=
| (1+2k-1)k |
| 2 |
| 2(1-3k) |
| 1-3 |
(3)在数列{an}中,仅存在连续的三项a1,a2,a3,按原来的顺序成等差数列,此时正整数m的值为1,下面说明理由
若am=a2k,则由am+am+2=2am+1,得2×3k-1+2×3k=2(2k+1).
化简得4•3k-1=2k+1,此式左边为偶数,右边为奇数,不可能成立.
若am=a2k-1,则由am+am+2=2am+1,得(2k-1)+(2k+1)=2×2×3k-1
化简得k=3k-1,
令Tk=
| k |
| 3k-1 |
| k+1 |
| 3k |
| k |
| 3k-1 |
| 1-2k |
| 3k |
因此,1=T1>T2>T3>…,故只有T1=1,此时K=1,m=2×1-1=1.
综上,在数列{an}中,仅存在连续的三项a1,a2,a3,按原来的顺序成等差数列,此时正整数m的值为1.
点评:本题考查了等差数列与等比数列的通项公式性质及其前n项和公式等基础知识与基本方法,属于难题.

练习册系列答案
相关题目
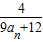 ,求f(0)+f(
,求f(0)+f(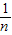 )+f(
)+f(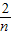 )+…+f(
)+…+f(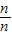 );
);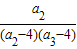 +
+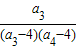 +…+
+…+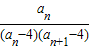 ≥
≥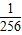 (1-
(1-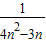 ).
). ,求cn=f(0)+f(
,求cn=f(0)+f( )+f(
)+f( )+…+f(
)+…+f( ),求
),求 +
+ +…+
+…+ 的值.
的值.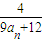 ,求f(0)+f(
,求f(0)+f(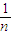 )+f(
)+f(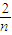 )+…+f(
)+…+f(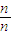 );
);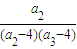 +
+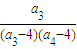 +…+
+…+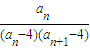 ≥
≥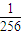 (1-
(1-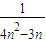 ).
).