Question

设函数f(x)的定义域为[－1，0]∪(0，1)，且f(－x)＝－f(x)恒成立，当x∈(0，1)时，f(x)＝2ax－(a∈R)．

(1)求当x∈[－1，0]时，f(x)的解析式；

(2)若f(x)在[－1，0]上为增函数，求实数a的取值范围；

(3)若f(x)在区间[－1，0)上的最小值为12，求a的值．

Answer 1

答案：
解析：

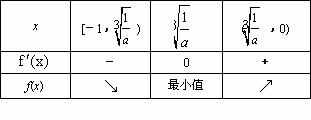
解：(1)x∈[－1，0]，则－x∈(0，1)，从而f(－x)＝2a(－x)－＝－f(x)， 　　∴f(x)＝2ax＋．………………………………………………………4分 　　(2)f(x)在[－1，0]上为增函数， 　　∴f ′(x)＝2a－≥0在x∈[－1，0]上恒成立， 　　即a≥在[－1，0]上恒成立．又－1≤x＜0， 　　∴≤－1， 　　∴a≥－1……………8分 　　(3)当a≥－1时，f(x)在[－1，0]上单调递增， 　　∴f(x)min＝f(－1)＝－2a＋1＝12， 　　∴a＝－，舍 　　当a＜－1时，令f ′(x)＝2a－＝0得x＝ 　　∴f(x)min＝ f()＝2a＋＝3＝12， 　　∴a2＝26，又a＜－1， 　　∴a＝－8……………………………………………………14分