题目内容
二次函数y=f（x）的图象过坐标原点，且其导函数的图象过二、三、四象限，则函数y=f（x）的图象不经过
- A.第一象限
- B.第二象限
- C.第三象限
- D.第四象限
A
分析：设二次函数y=f（x）=ax2+bx，利用它的导数y=f′（x）=2ax+b 图象过二、三、四象限，可得a＜0，b＜0，y=f（x）的图象顶点 （-
，
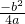）在第二象限．
解答：由题意可知可设二次函数y=f（x）=ax2+bx，它的导数y=f′（x）=2ax+b，
由导数y=f′（x）的图象是经过二、三、四象限的一条直线，
∴a＜0，b＜0，
y=f（x）的图象顶点 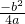（-， ）在第二象限，
故选 A．
点评：本题考查求函数的导数的方法，直线在坐标系中的位置与斜率、截距的关系，二次函数的性质．
分析：设二次函数y=f（x）=ax2+bx，利用它的导数y=f′（x）=2ax+b 图象过二、三、四象限，可得a＜0，b＜0，y=f（x）的图象顶点 （-
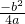， ）在第二象限．解答：由题意可知可设二次函数y=f（x）=ax2+bx，它的导数y=f′（x）=2ax+b，
由导数y=f′（x）的图象是经过二、三、四象限的一条直线，
∴a＜0，b＜0，
y=f（x）的图象顶点 （-
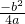， ）在第二象限，故选 A．
点评：本题考查求函数的导数的方法，直线在坐标系中的位置与斜率、截距的关系，二次函数的性质．
练习册系列答案
相关题目
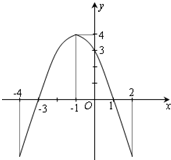如图是一个二次函数y=f（x）的图象．
已知二次函数y=f（x）的图象如图所示．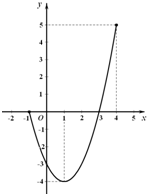
二次函数y=f（x）的图象的一部分如图所示．