题目内容
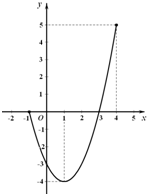 二次函数y=f(x)的图象的一部分如图所示.
二次函数y=f(x)的图象的一部分如图所示.(Ⅰ)根据图象写出f(x)在区间[-1,4]上的值域;
(Ⅱ)根据图象求y=f(x)的解析式;
(Ⅲ)试求k的范围,使方程f(x)-k=0在(-1,4]上的解集恰为两个元素的集合.
分析:(Ⅰ)根据图象的最低点与最高点得出f(x)的值域.
(Ⅱ)由图象与x轴交点,用待定系数法求出f(x)的解析式.
(Ⅲ)方法1,构造函数g(x)=f(x)-k,判定二次函数g(x)在(-1,4]上有两个零点即可;
方法2,由原方程的解与函数y=x2-2x-3,x∈(-1,4]和y=k的图象的交点有两个,结合图象得出结论.
(Ⅱ)由图象与x轴交点,用待定系数法求出f(x)的解析式.
(Ⅲ)方法1,构造函数g(x)=f(x)-k,判定二次函数g(x)在(-1,4]上有两个零点即可;
方法2,由原方程的解与函数y=x2-2x-3,x∈(-1,4]和y=k的图象的交点有两个,结合图象得出结论.
解答:解:(Ⅰ)由图象知,图象最低点f(1)=-4,最高点f(4)=5,
∴f(x)在区间[-1,4]上的值域为[-4,5].
(Ⅱ)根据图象设y=a(x+1)(x-3),
即y=a(x2-2x-3),
因为图象过点(1,-4),所以a(1-2-3)=-4.
解得a=1.
所以二次函数的解析式为y=f(x)=x2-2x-3.
(Ⅲ)方法1:设g(x)=f(x)-k=x2-2x-3-k,
依条件有
,
即
,
解得-4<k<0;
∴k的取值范围是{k|-4<k<0}.
方法2:∵原方程的解与两个函数y=x2-2x-3,x∈(-1,4]和y=k的图象的交点构成一一对应.
∴由图象知,当-4<k<0时,原方程在(-1,4]上的解集为两元素集合,
∴k的取值范围是{k|-4<k<0}.
∴f(x)在区间[-1,4]上的值域为[-4,5].
(Ⅱ)根据图象设y=a(x+1)(x-3),
即y=a(x2-2x-3),
因为图象过点(1,-4),所以a(1-2-3)=-4.
解得a=1.
所以二次函数的解析式为y=f(x)=x2-2x-3.
(Ⅲ)方法1:设g(x)=f(x)-k=x2-2x-3-k,
依条件有
|
即
|
解得-4<k<0;
∴k的取值范围是{k|-4<k<0}.
方法2:∵原方程的解与两个函数y=x2-2x-3,x∈(-1,4]和y=k的图象的交点构成一一对应.
∴由图象知,当-4<k<0时,原方程在(-1,4]上的解集为两元素集合,
∴k的取值范围是{k|-4<k<0}.
点评:本题考查了二次函数的图象与性质的应用问题,解题时能数形结合,有助于解题,是中档题.

练习册系列答案
相关题目
 如图是一个二次函数y=f(x)的图象.
如图是一个二次函数y=f(x)的图象. 已知二次函数y=f(x)的图象如图所示.
已知二次函数y=f(x)的图象如图所示.