题目内容
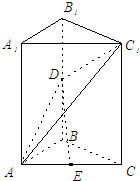 如图所示,在直三棱柱ABC-A1B1C1中,已知AB=BC=1,∠ABC=90°,
如图所示,在直三棱柱ABC-A1B1C1中,已知AB=BC=1,∠ABC=90°,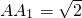 ,D,E分别为BB1、AC的中点
,D,E分别为BB1、AC的中点
(Ⅰ)证明:BE∥平面AC1D;
(Ⅱ)求二面角A1-AD-C1的大小.
(Ⅰ)证明:以BA所在的直线为x轴,BC所在的直线为y轴,BB1所在的直线为z轴,建立空间直角坐标系,则A(1,0,0),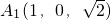 ,
,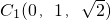 ,
,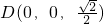 ,
,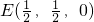 ,
,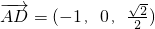 ,
,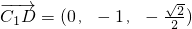 ,
,
设平面AC1D的一个法向量为 ,
,
则由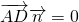 和
和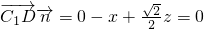 ,
,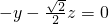 ,
,
取x=1,y=-1,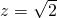 ,所以法向量
,所以法向量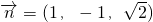 ,
,
又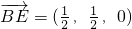 ,
,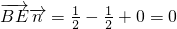 ,
,
因为 ?平面AC1D,所以BE∥平面AC1D.
?平面AC1D,所以BE∥平面AC1D.
(Ⅱ)由(1)可知,平面AC1D的法向量为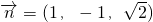 .
.
又平面A1AD的法向量为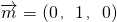 ,所以
,所以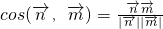 =
=
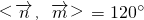 ,
,
由图可知,所求的二面角为锐角,所以二面角A1-AD-C1的大小为60°.
分析:(Ⅰ)以BA所在的直线为x轴,BC所在的直线为y轴,BB1所在的直线为z轴,建立空间直角坐标系,先求平面AC1D的一个法向量,再证明: 即可;
即可;
(Ⅱ)求二面角A1-AD-C1的大小,只需求两平面的法向量的夹角即可.
点评:本题以直三棱柱为载体,考查线面平行,考查面面角,关键是建立空间直角坐标系,用坐标表示向量.
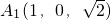 ,
,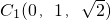 ,
,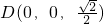 ,
,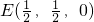 ,
,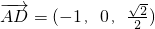 ,
,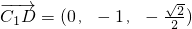 ,
,设平面AC1D的一个法向量为
 ,
,则由
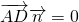 和
和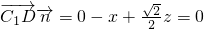 ,
,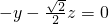 ,
,取x=1,y=-1,
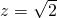 ,所以法向量
,所以法向量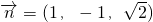 ,
,又
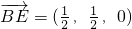 ,
,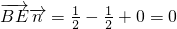 ,
,因为
 ?平面AC1D,所以BE∥平面AC1D.
?平面AC1D,所以BE∥平面AC1D.(Ⅱ)由(1)可知,平面AC1D的法向量为
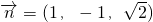 .
.又平面A1AD的法向量为
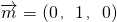 ,所以
,所以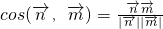 =
=
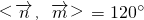 ,
,由图可知,所求的二面角为锐角,所以二面角A1-AD-C1的大小为60°.
分析:(Ⅰ)以BA所在的直线为x轴,BC所在的直线为y轴,BB1所在的直线为z轴,建立空间直角坐标系,先求平面AC1D的一个法向量,再证明:
 即可;
即可;(Ⅱ)求二面角A1-AD-C1的大小,只需求两平面的法向量的夹角即可.
点评:本题以直三棱柱为载体,考查线面平行,考查面面角,关键是建立空间直角坐标系,用坐标表示向量.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AA1=AC=BC=2,D、E、F分别是AB、AA1、CC1的中点,P是CD上的点.
如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AA1=AC=BC=2,D、E、F分别是AB、AA1、CC1的中点,P是CD上的点. 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=
如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF= 如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1,AC1⊥平面A1BD,D为AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1,AC1⊥平面A1BD,D为AC的中点. 如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1=BC,AC1⊥平面A1BD,D为AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1=BC,AC1⊥平面A1BD,D为AC的中点.