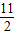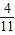题目内容
点P在直径为5的球面上,过P作两两垂直的3条弦,设长度分别为a、b、c.若这三条弦总长为6,以点P为顶点,这三条弦为侧棱的三棱锥的体积为
,则
+
+
=( )
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
分析:由点P在直径为5的球面上,过P作两两垂直的3条弦,推出这三条弦为侧棱的三棱锥是长方体的一个角的三棱锥,A-BCD,如图,三棱锥扩展为长方体,它们的外接球是一个,通过已知的数据关系,列出方程组,求出a,b,c即可确定
+
+
的值.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
解答:解:由题意可知:三条弦为侧棱的三棱锥是长方体的一个角的三棱锥,如图三棱锥A-BCD,扩展为长方体,它们的外接球是一个,长方体的体对角线就是外接球的直径,因为点P在直径为5的球面上,过P作两两垂直的3条弦,
设长度分别为a、b、c.若这三条弦总长为6,以点P为顶点,这三条弦为侧棱的三棱锥的体积为
,
所以
,即
①2-②2ab+2bc+2ac=11…④,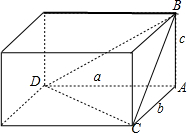
由
得
=
,所以
+
+
=
.
故选D.
设长度分别为a、b、c.若这三条弦总长为6,以点P为顶点,这三条弦为侧棱的三棱锥的体积为
| 1 |
| 3 |
所以
|
|
①2-②2ab+2bc+2ac=11…④,

由
| ④ |
| ③ |
| 2ab+2bc+2ac |
| abc |
| 11 |
| 2 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 11 |
| 4 |
故选D.
点评:本题考查几何体的外接球的理解,能够把三棱锥扩展为长方体,外接球相同是解题的关键,考查计算能力整体思想的应用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
点P在直径为
的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是( )
| 6 |
A、
| ||||
| B、6 | ||||
C、
| ||||
D、
|
 ,则
,则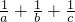 =
=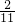

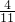

 ,则
,则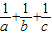 =( )
=( )