题目内容
点P在直径为2的球面上,过P两两垂直的3条弦,若其中一条弦长是另一条的2倍,则这3条弦长之和的最大值是分析:设三条弦长分别为x,2x,y,求出长方体的对角线的长,用椭圆的参数方程表示x,y,推出3条弦长之和的表达式,通过三角函数的化简辅助角公式,求出最大值.
解答:解:设三条弦长分别为x,2x,y,则:x2+(2x)2+y2=4,即:5x2+y2=4,设
x=sinθ,
y=cosθ,则这3条弦长之和=3x+y=
sinθ +2cosθ=
sin(θ+φ),其中tanφ=
,所以它的最大值为:
故答案为:
| ||
| 2 |
| 1 |
| 2 |
| 6 | ||
|
2
| ||
| 5 |
| ||
| 3 |
2
| ||
| 5 |
故答案为:
2
| ||
| 5 |
点评:本题是中档题,考查球的内接多面体的就是问题,三角函数的化简与求值,是综合题目,考查计算能力,空间想象能力.

练习册系列答案
相关题目
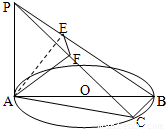
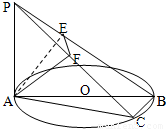
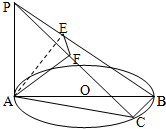 如图,AB为圆O的直径,点C为圆O上异于A、B的一点,PA⊥平面ABC,点A在PB、PC上的射影分别为点E、F.
如图,AB为圆O的直径,点C为圆O上异于A、B的一点,PA⊥平面ABC,点A在PB、PC上的射影分别为点E、F.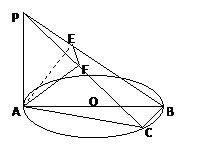
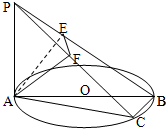 如图,AB为圆O的直径,点C为圆O上异于A、B的一点,PA⊥平面ABC,点A在PB、PC上的射影分别为点E、F.
如图,AB为圆O的直径,点C为圆O上异于A、B的一点,PA⊥平面ABC,点A在PB、PC上的射影分别为点E、F.