题目内容
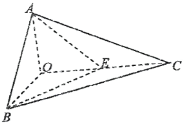
【题目】如图,已知三棱锥O—ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
(1)求异面直线BE与AC所成角的余弦值;
(2)求二面角A—BE—C的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() 。
。
【解析】
(1)先以O为原点,OB,OC,OA分别为x,y,z轴建立空间直角坐标系.设出点的坐标,求出直线直线BE与AC的方向向量,最后利用向量的夹角公式计算即得异面直线BE与AC所成的角的余弦值;
(2)先分别求得平面ABE的法向量和平面BEC的一个法向量,再利用夹角公式求二面角的余弦值即可.
(1)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则有![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]() .
.

![]() .
.
由于异面直线![]() 与
与![]() 所成的角是锐角,故其余弦值是
所成的角是锐角,故其余弦值是![]() .
.
(2)![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则由![]() ,得
,得![]()
取![]() .
.
同理可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() .
.
由于二面角![]() 的平面角是
的平面角是![]() 与
与![]() 的夹角的补角,其余弦值是
的夹角的补角,其余弦值是![]() .
.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目