题目内容
已知动点P到定点F(0,1)的距离等于点P到定直线l:y=-1的距离.点M是F关于原点的对称点.
(1)求动点P的轨迹C的方程;
(2)过点M作轨迹C的切线,若切点在第一象限,求切线m的方程;
(3)试探究(2)中直线m与动圆x2+(y-b)2=5,b∈R的位置关系.
答案:
解析:
解析:
解:(1)依题意,动点![]() 的轨迹为焦点
的轨迹为焦点![]() 的抛物线,
的抛物线,
∴抛物线![]() 的方程为
的方程为![]() . 3分
. 3分
(2)设切点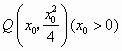 .由
.由![]() ,知抛物线在
,知抛物线在![]() 点处的切线斜率为
点处的切线斜率为![]() ,
,
∴所求切线方程![]() ,
,
即![]() .
.
∵![]() 的焦点
的焦点![]() 关于原点的对称点
关于原点的对称点![]() .
.
∴点![]() 在切线上,
在切线上,
∴![]() ,
,
∴![]() 或
或![]() (舍去).
(舍去).
∴所求切线方程为![]() . 8分
. 8分
(3)依题意,动圆的半径为![]() ,
,
圆心![]() 到直线
到直线![]() 的距离
的距离![]() .
.
若![]() ,即
,即![]() ,∴
,∴![]() 或
或![]() 时,
时,![]() 与动圆相离;
与动圆相离;
‚
若![]() ,即
,即![]() ,∴
,∴![]() 或
或![]() 时,
时,![]() 与动圆相切;
与动圆相切;
ƒ
若![]() ,即
,即![]() ,∴
,∴![]() 或
或![]() 时,
时,![]() 与动圆相交. 14分
与动圆相交. 14分

练习册系列答案
相关题目
 , 0 ) 的距离与点 P 到定直线 l:x=2
, 0 ) 的距离与点 P 到定直线 l:x=2 。
。 ·
· =0,
=0,
 , 0 ) 的距离与点 P 到定直线 l:x=2
, 0 ) 的距离与点 P 到定直线 l:x=2 。
。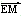 ·
· =0,
=0,