题目内容
已知动点P到定点F(0,-2)的距离和它到定直线l:y=-6的距离之比为| 1 | 3 |
分析:设出动点的坐标,将已知条件中的几何关系用坐标表示,化简方程,据椭圆方程的形式判断出动点的轨迹形状.
解答:解:设P(x,y),依题意有
=
,
化简得,9x2+8y2+24y=0,即
+
=1.
轨迹是中心为(0,-
),F为一个焦点,l为相应准线的椭圆.
| ||
| |y-(-6)| |
| 1 |
| 3 |
化简得,9x2+8y2+24y=0,即
| x2 |
| 2 |
(y+
| ||
|
轨迹是中心为(0,-
| 3 |
| 2 |
点评:判断动点的轨迹问题常常通过求出动点的轨迹方程,据方程的特殊形式判断出动点的轨迹.

练习册系列答案
相关题目
 , 0 ) 的距离与点 P 到定直线 l:x=2
, 0 ) 的距离与点 P 到定直线 l:x=2 。
。 ·
· =0,
=0,
 , 0 ) 的距离与点 P 到定直线 l:x=2
, 0 ) 的距离与点 P 到定直线 l:x=2 。
。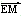 ·
· =0,
=0,