题目内容
已知二次函数 为常数,且
为常数,且 )满足条件:
)满足条件: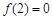 ,且方程
,且方程 有两个相等的实数根.
有两个相等的实数根.
(1)求 的解析式;
的解析式;
(2)求函数在区间 上的最大值和最小值;
上的最大值和最小值;
(3)是否存在实数
 使
使 的定义域和值域分别为
的定义域和值域分别为 和
和 ,如果存在,求出
,如果存在,求出 的值,如不存在,请说明理由.
的值,如不存在,请说明理由.
【答案】
(1)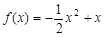 ;(2)最大值
;(2)最大值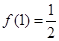 ,最小值
,最小值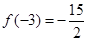 (3)存在
(3)存在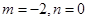 满足题设条件。
满足题设条件。
【解析】
试题分析:(1)∵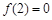 ,∴
,∴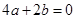 ,又方程
,又方程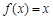 有两个相等的实数根,∴
有两个相等的实数根,∴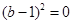 ,∴
,∴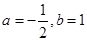 ,∴
,∴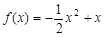 ;(2)∵
;(2)∵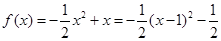 ,∴当x=1时,函数f(x)有最大值
,∴当x=1时,函数f(x)有最大值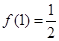 ,当x=-3时,函数f(x)有最小值
,当x=-3时,函数f(x)有最小值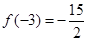 (3) 由(2)知,m=1时,不合题意,故
(3) 由(2)知,m=1时,不合题意,故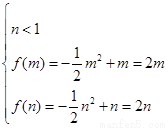 或
或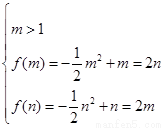 ,∴
,∴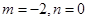 ,∴存在
,∴存在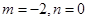 满足题设条件。
满足题设条件。
考点:本题考查了一元二次函数求法及最值的运用
点评:二次函数 在闭区间
在闭区间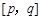 上的最值可能出现以下三种情况:(1)若
上的最值可能出现以下三种情况:(1)若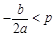 ,则
,则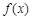 在区间
在区间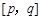 上是增函数,则
上是增函数,则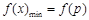 ,
,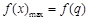 ;(2)若
;(2)若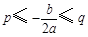 ,则
,则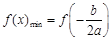 . 此时
. 此时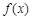 的最大值视对称轴与区间端点的远近而定:①当
的最大值视对称轴与区间端点的远近而定:①当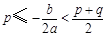 时,
时,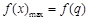 ;②当
;②当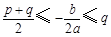 时,
时, .(3)若
.(3)若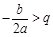 ,则
,则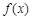 在区间
在区间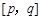 上是减函数,则
上是减函数,则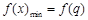 ,
, .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 .若直线
.若直线 1、
1、 的图象以及
的图象以及 、b、c的值;
、b、c的值; 问是否存在实数m,使得
问是否存在实数m,使得 的图象与
的图象与 的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
 (
( 为常数).
为常数). 是偶函数,求
是偶函数,求 ,求函数
,求函数 的任意正实数
的任意正实数 ,都有
,都有 ,求实数
,求实数 的取值范围。
的取值范围。