题目内容
如果函数 的导函数的图像如图所示,给出下列判断:
的导函数的图像如图所示,给出下列判断:
① 函数 在区间
在区间 内单调递增;
内单调递增;
②函数 在区间
在区间 内单调递减;
内单调递减;
③函数 在区间
在区间 内单调递增;
内单调递增;
④当 时,函数
时,函数 有极大值;
有极大值;
⑤当 时,函数
时,函数 有极大值;
有极大值;
则上述判断中正确的是 .
③⑤
解析试题分析:观察导函数的图像可得,当 或
或 时,
时, ,而当
,而当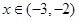 或
或 时,
时, ,所以
,所以 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 ,
, ,所以③正确,①②错误;由
,所以③正确,①②错误;由 在
在 单调递增,在
单调递增,在 单调递减,所以当
单调递减,所以当 时,函数
时,函数 有极大值,所以⑤正确,由
有极大值,所以⑤正确,由 在
在 单调递增,所以
单调递增,所以 不是极值点,故④错误,综上可知③⑤正确.
不是极值点,故④错误,综上可知③⑤正确.
考点:1.函数的单调性与导数;2.函数的极值与导数.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 的图象如图所示,则
的图象如图所示,则 .
.
 ,且
,且 ,求
,求 的值。
的值。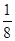 ,则sin θ-cos θ的值为________.
,则sin θ-cos θ的值为________. 是第四象限的角,则
是第四象限的角,则 = .
= . 则
则
 具备的性质有 . (将所有符合题意的序号都填上)
具备的性质有 . (将所有符合题意的序号都填上) 是偶函数;
是偶函数; ;
; 上是增加的;
上是增加的; =________.
=________.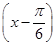 的图象,则φ=________.
的图象,则φ=________.