题目内容
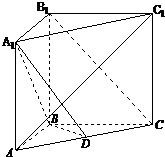16、如图所示，在直三棱柱ABC-A1B1C1中，AB=A1B1，AC1⊥平面A1BD，D为AC的中点．（Ⅰ）求证：B1C∥平面A1BD；（Ⅱ）求证：B1C1⊥平面ABB1A1；
分析：（I）由中位线定理得到B1C∥MD，再由线面平行的判定理理得到B1C∥平面A1BD；
（Ⅱ）先证明A1B⊥B1C1，BB1⊥B1C1求再由线面垂直的判定理得到B1C1⊥平面ABB1A1．
（Ⅱ）先证明A1B⊥B1C1，BB1⊥B1C1求再由线面垂直的判定理得到B1C1⊥平面ABB1A1．
解答：（Ⅰ）证明：如图，连接AB1与A1B相交于M，则M为A1B的中点，
连接MD，D又为AC的中点，
∴B1C∥MD．
又B1C不包含于平面A1BD，MD?平面A1BD，B1C∥平面A1BD
∴B1C∥平面A1BD．（5分）
（Ⅱ）∵AB=B1B∴四边形ABB1A1为正方形
∴A1B⊥AB1
又∵AC1⊥面A1BD，∴AC1⊥A1B，
∴A1B⊥面AB1C1，
∴A1B⊥B1C1，
又在直棱柱ABC-A1B1C1中BB1⊥B1C1，
∴B1C1⊥平面ABB1A1（9分）
连接MD，D又为AC的中点，
∴B1C∥MD．
又B1C不包含于平面A1BD，MD?平面A1BD，B1C∥平面A1BD
∴B1C∥平面A1BD．（5分）
（Ⅱ）∵AB=B1B∴四边形ABB1A1为正方形
∴A1B⊥AB1
又∵AC1⊥面A1BD，∴AC1⊥A1B，
∴A1B⊥面AB1C1，
∴A1B⊥B1C1，
又在直棱柱ABC-A1B1C1中BB1⊥B1C1，
∴B1C1⊥平面ABB1A1（9分）
点评：本题主要考查线面平行和线面垂直的判定定理以及三角形中位线定理．
练习册系列答案
相关题目
如图所示，在直三棱柱ABC-A1B1C1中，AC⊥BC，AA1=AC=BC=2，D、E、F分别是AB、AA1、CC1的中点，P是CD上的点．
如图所示，在直三棱柱ABC-A′B′C′中，∠BAC=90°，AB=BB′=1，直线B′C与平面ABC成30°角．
如图所示，在直三棱柱ABC-A1B1C1中，底面是∠ABC为直角的等腰直角三角形，AC=2a，BB1=3a，D是A1C1的中点，点F在线段AA1上，当AF=
如图所示，在直三棱柱ABC-A1B1C1中，AB=BB1，AC1⊥平面A1BD，D为AC的中点．
如图所示，在直三棱柱ABC-A1B1C1中，AB=BB1=BC，AC1⊥平面A1BD，D为AC的中点．