题目内容
等比数列{ }的前n项和为
}的前n项和为 , 已知对任意的
, 已知对任意的 ,点
,点 均在函数
均在函数 (
( 且
且 ,b,r均为常数)的图像上。
,b,r均为常数)的图像上。
(1)求r的值;
(2)当b=2时,记 ,证明:对任意的
,证明:对任意的 ,不等式
,不等式 成立。
成立。
 }的前n项和为
}的前n项和为 , 已知对任意的
, 已知对任意的 ,点
,点 均在函数
均在函数 (
( 且
且 ,b,r均为常数)的图像上。
,b,r均为常数)的图像上。(1)求r的值;
(2)当b=2时,记
 ,证明:对任意的
,证明:对任意的 ,不等式
,不等式 成立。
成立。 (1)解: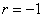 ;
;
(2)证明:当b=2时,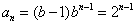 ,
,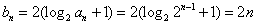 ,
,
则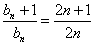 ,
,
所以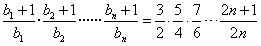 ,
,
下面用数学归纳法证明不等式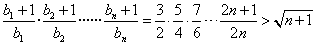 成立。
成立。
①当n=1时,左边=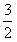 ,右边=
,右边= ,因为
,因为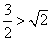 ,所以不等式成立;
,所以不等式成立;
②假设当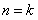 时,不等式成立,即
时,不等式成立,即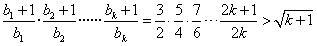 成立,
成立,
则当 时,下面证明
时,下面证明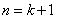 时,不等式:
时,不等式: 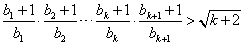 成立,
成立,
左边=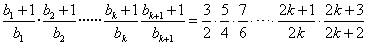
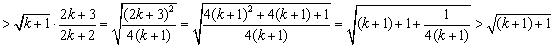 ,
,
所以当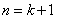 时,不等式也成立。
时,不等式也成立。
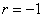 ;
;(2)证明:当b=2时,
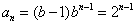 ,
,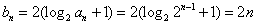 ,
,则
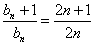 ,
,所以
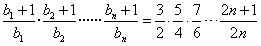 ,
,下面用数学归纳法证明不等式
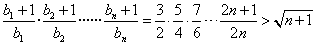 成立。
成立。①当n=1时,左边=
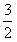 ,右边=
,右边= ,因为
,因为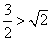 ,所以不等式成立;
,所以不等式成立;②假设当
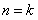 时,不等式成立,即
时,不等式成立,即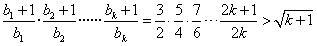 成立,
成立,则当
 时,下面证明
时,下面证明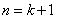 时,不等式:
时,不等式: 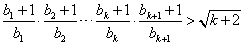 成立,
成立,左边=
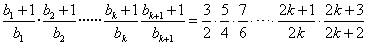
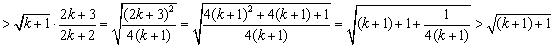 ,
,所以当
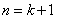 时,不等式也成立。
时,不等式也成立。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目