题目内容
设直线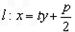 与抛物线C:
与抛物线C: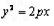 (
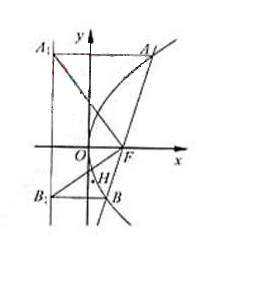
(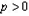 ,p为常数)交于不同两点A、B,点D为抛物线准线上的一点。
,p为常数)交于不同两点A、B,点D为抛物线准线上的一点。
(I)若t=0,且三角形ABD的面积为4,求抛物线的方程;
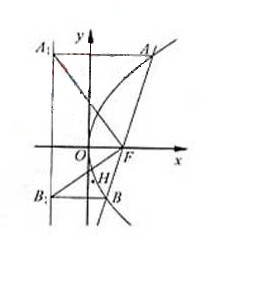
(II)当△ABD为正三角形时,求出点D的坐标。
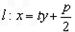 与抛物线C:
与抛物线C: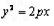 (
(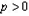 ,p为常数)交于不同两点A、B,点D为抛物线准线上的一点。
,p为常数)交于不同两点A、B,点D为抛物线准线上的一点。(I)若t=0,且三角形ABD的面积为4,求抛物线的方程;
(II)当△ABD为正三角形时,求出点D的坐标。
解:(I)直线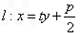 过焦点
过焦点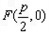
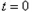 时,
时,
不妨设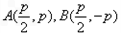 ,则
,则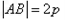 ,
,
又D点到直线l的距离d=p 所以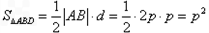 =4∴p=2
=4∴p=2
∴抛物线的方程为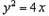
(II)设
由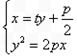 得
得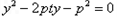 则
则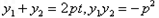
从而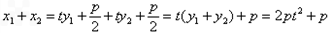
∴线段AB的中点为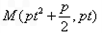
由DM⊥AB得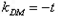 ,即
,即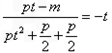 ,
,
解得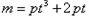 从而
从而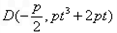
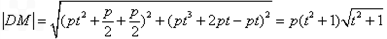
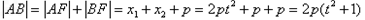
由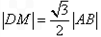 得到
得到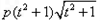 =
= 
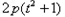 ,
,
解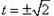
此时,点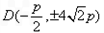
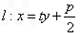 过焦点
过焦点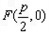
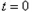 时,
时,不妨设
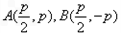 ,则
,则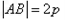 ,
,又D点到直线l的距离d=p 所以
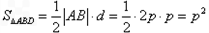 =4∴p=2
=4∴p=2∴抛物线的方程为
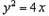
(II)设

由
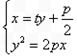 得
得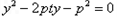 则
则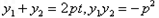
从而
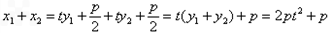
∴线段AB的中点为
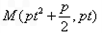
由DM⊥AB得
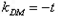 ,即
,即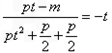 ,
,解得
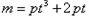 从而
从而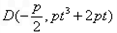
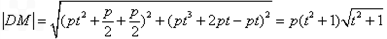
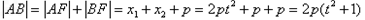
由
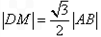 得到
得到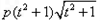 =
= 
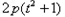 ,
,解
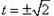
此时,点
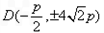

练习册系列答案
相关题目
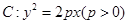 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.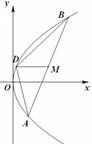
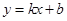 与抛物线C交于两点
与抛物线C交于两点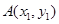 ,
,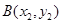 ,且
,且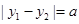 (a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到
(a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到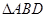 .
. 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5. 与抛物线C交于两点
与抛物线C交于两点 ,
, ,且
,且 (
( ,且
,且 为常数).过弦AB的中点M作平行于
为常数).过弦AB的中点M作平行于 轴的直线交抛物线于点D,连结AD、BD得到
轴的直线交抛物线于点D,连结AD、BD得到 .
. ;
; 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.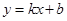 与抛物线C交于两点
与抛物线C交于两点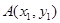 ,
,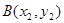 ,且
,且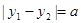 (
(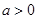 ,且
,且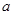 为常数).过弦AB的中点M作平行于
为常数).过弦AB的中点M作平行于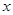 轴的直线交抛物线于点D,连结AD、BD得到
轴的直线交抛物线于点D,连结AD、BD得到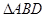 .
.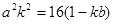 ;
;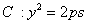 (p>0)
(p>0)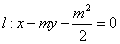 上。
上。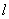 与抛物线C交于A、B,△A
与抛物线C交于A、B,△A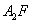 ,△
,△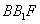 的重心分别为G,H
的重心分别为G,H