题目内容
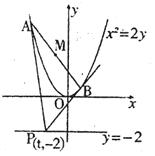
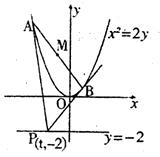
如图,已知抛物线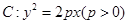 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设直线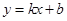 与抛物线C交于两点
与抛物线C交于两点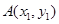 ,
,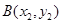 ,且
,且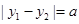 (a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到
(a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到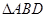 .
.
(i)求实数a,b,k满足的等量关系;
(ii)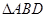 的面积是否为定值?若为定值,求出此定值;若不是定值,请说明理由.
的面积是否为定值?若为定值,求出此定值;若不是定值,请说明理由.
【答案】
(Ⅰ)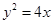 (Ⅱ)(i)
(Ⅱ)(i) (ii)为定值
(ii)为定值
【解析】
试题分析:(Ⅰ)依题意: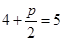 ,解得
,解得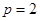 .
.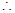 抛物线方程为
抛物线方程为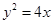 .
.
(Ⅱ)(i)由方程组 消去
消去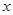 得:
得: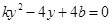 .(※)
.(※)
依题意可知: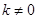 .
.
由已知得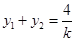 ,
,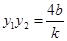 .
.
由 ,得
,得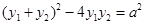 ,即
,即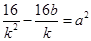 ,整理得
,整理得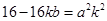 .
.
所以 .
.
(ii)由(i)知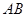 中点
中点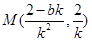 ,所以点
,所以点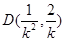 ,
,
依题意知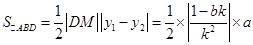 .
.
又因为方程(※)中判别式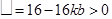 ,得
,得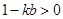 .
.
所以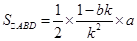 ,
,
由(Ⅱ)可知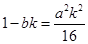 ,所以
,所以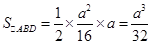 .
.
又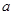 为常数,故
为常数,故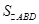 的面积为定值.
的面积为定值.
考点:本小题主要考查抛物线标准方程的求解,直线与抛物线的位置关系的判断和应用,三角形面积公式的应用,考查学生的运算求解能力.
点评:判断直线与抛物线的位置关系时,不要忘记验证判别式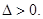

练习册系列答案
相关题目
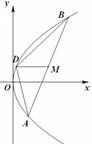
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).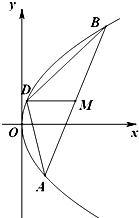 如图,已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.
如图,已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.