题目内容
已知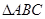 中,
中, ,
, ,
, 为
为 的中点,
的中点,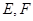 分别在线段
分别在线段 上,且
上,且
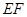 交
交 于
于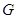 ,把
,把 沿
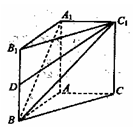
沿 折起,如下图所示,
折起,如下图所示,

(1)求证: 平面
平面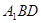 ;
;
(2)当二面角 为直二面角时,是否存在点
为直二面角时,是否存在点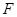 ,使得直线
,使得直线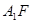 与平面
与平面 所成的角为
所成的角为 ,若存在求
,若存在求 的长,若不存在说明理由.
的长,若不存在说明理由.
(1)证明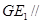 平面
平面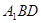 ,及
,及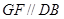 ,则
,则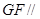 平面
平面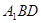 ,得到平面
,得到平面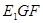 //平面
//平面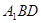 ,
,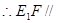 平面
平面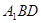 .
.
(2)存在点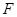 ,使得直线
,使得直线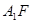 与平面
与平面 所成的角为
所成的角为 ,且
,且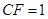 .
.
解析试题分析:(1)证明“线面平行”,一般思路是通过证明“线线平行”或“面面平行”.本题中,注意到平面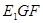 与平面
与平面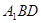 的平行关系易得,因此,通过证明“面面平行”,达到目的.
的平行关系易得,因此,通过证明“面面平行”,达到目的.
(2)存在性问题,往往通过“找,证”等,实现存在性的证明.本题从确定二面角的平面角入手,同时确定得到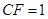 .
.
试题解析:(1)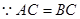 ,又
,又 为
为 的中点
的中点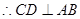 ,又
,又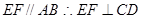 2分
2分
在空间几何体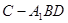 中,
中,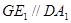 ,则
,则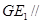 平面
平面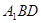
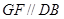 ,则
,则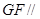 平面
平面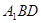
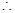 平面
平面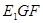 //平面
//平面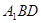 5分
5分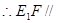 平面
平面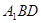 7分
7分
(2)∵二面角 为直二面角,
为直二面角,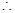 平面
平面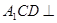 平面
平面
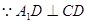 ,
,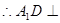 平面
平面 , 9分
, 9分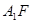 在平面
在平面 内的射影为
内的射影为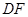 ,
,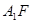 与平面
与平面 所成角为
所成角为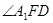 ,
,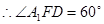 11分
11分
由于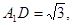
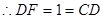 ,
,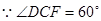
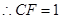 14分
14分
考点:平行关系,垂直关系,二面角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中,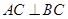 ,点D是AB的中点,
,点D是AB的中点,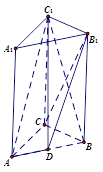
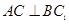 ; (2)
; (2)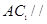 平面
平面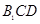
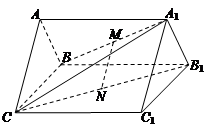
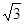 ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小  ,
, ,
,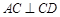 ,
,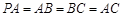 ,
, 是
是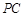 的中点.
的中点.
 ;
; 的平面角的正弦值.
的平面角的正弦值.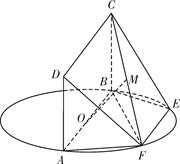

 中,
中,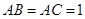 ,
,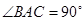 ,异面直线
,异面直线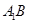 与
与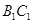 所成
所成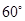 .
.
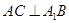 ;
;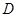 是
是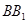 的中点,求
的中点,求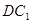 与平面
与平面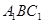 所成角的正弦值.
所成角的正弦值.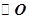 的直径,D为
的直径,D为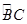 的中点,E为BC的中点.
的中点,E为BC的中点.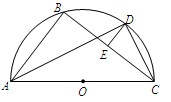
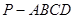 中,
中,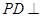 底面
底面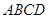 ,面
,面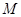 为侧棱
为侧棱 上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
上一点.该四棱锥的俯视图和侧(左)视图如图2所示. 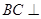 平面
平面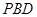 ;
; 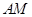 ∥平面
∥平面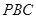 ;
; 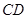 上是否存在点
上是否存在点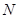 ,使
,使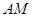 与
与 所成角的余弦值为
所成角的余弦值为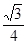 ?若存在,找到所有符合要求的点
?若存在,找到所有符合要求的点 的长;若不存在,说明理由.
的长;若不存在,说明理由.