题目内容
数列{an}前n项和为Sn,a1=4,an+1=2Sn-2n+4.
(1)求证:数列{an-1}为等比数列;
(2)设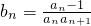 ,数列{bn}前n项和为Tn,求证:8Tn<1.
,数列{bn}前n项和为Tn,求证:8Tn<1.
证明:(1)∵an+1=2Sn-2n+4,∴n≥2时,an=2Sn-1-2(n-1)+4
∴n≥2时,an+1=3an-2(2分)
又a2=2S1-2+4=10,∴n≥1时an+1=3an-2(4分)
∵a1-1=3≠0,∴an-1≠0,
∴ ,∴数列{an-1}为等比数列 (6分)
,∴数列{an-1}为等比数列 (6分)
(2)由(1)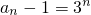 ,∴
,∴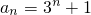 ,
,
∴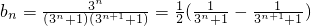 (9分)
(9分)
∴ =
=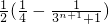 (11分)
(11分)
∴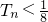 ,
,
∴8Tn<1(12分)
分析:(1)利用数列递推式,再写一式,两式相减,可证数列{an-1}为等比数列;
(2)确定数列{bn}的通项,利用裂项法求前n项和为Tn,即可证得结论.
点评:本题考查等比数列的证明,考查裂项法求和,考查不等式的证明,确定数列的通项是关键.
∴n≥2时,an+1=3an-2(2分)
又a2=2S1-2+4=10,∴n≥1时an+1=3an-2(4分)
∵a1-1=3≠0,∴an-1≠0,
∴
 ,∴数列{an-1}为等比数列 (6分)
,∴数列{an-1}为等比数列 (6分)(2)由(1)
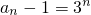 ,∴
,∴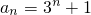 ,
,∴
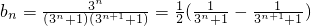 (9分)
(9分)∴
 =
=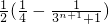 (11分)
(11分)∴
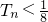 ,
,∴8Tn<1(12分)
分析:(1)利用数列递推式,再写一式,两式相减,可证数列{an-1}为等比数列;
(2)确定数列{bn}的通项,利用裂项法求前n项和为Tn,即可证得结论.
点评:本题考查等比数列的证明,考查裂项法求和,考查不等式的证明,确定数列的通项是关键.

练习册系列答案
相关题目