题目内容
(2007•武汉模拟)已知点(an,an-1)在曲线f(x)=
上,且a1=1.
(1)求f(x)的定义域;
(2)求证:
(n+1)
-1≤
+
+…+
≤4(n+1)
-1(n∈N*)
(3)求证:数列{an}前n项和Sn≤
-
(n≥1,n∈N*)
| |||
(1)求f(x)的定义域;
(2)求证:
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 2 |
| 3 |
(3)求证:数列{an}前n项和Sn≤
(3n+2)
| |||
| 2 |
| 3 |
| 2 |
分析:( 1)由f(x)=
知x满足:x2+
≥0,
≥0,所以
≥0.由此能够求出f(x)定义域.
(2)由an+12=an2+
,则an+12-an2=
,知
+
+…+
=an+12-a12=an+12-1.要证明:
(n+1)
-1≤
+
+…+
≤4(n+1)
-1,只需证明:
n
≤an≤2n
.由数学归纳法能够证明原不等式成立.
(3)要证明:Sn≤
-
,只需证:
<
-
(n≥2).用分析法可以证明Sn=a1+a2+…+an≤1+2(
+
+…+
)=
-
.
x2+
|
| 1 |
| x |
| x3+1 |
| x |
| (x+1)(x2-x+1) |
| x |
(2)由an+12=an2+
| 1 |
| an |
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
(3)要证明:Sn≤
(3n+2)
| |||
| 2 |
| 3 |
| 2 |
| 3 | n |
(3n+2)
| |||
| 4 |
[3(n-1)+2]
| |||
| 4 |
| 3 | 2 |
| 3 | 3 |
| 3 | n |
(3n+2)
| |||
| 2 |
| 3 |
| 2 |
解答:解:(1)由f(x)=
知x满足:x2+
≥0,
∴
≥0,
∴
≥0
∴
≥0,
故x>0,或x≤-1.
f(x)定义域为:(-∞,-1]∪(0,+∞).
(2)证明:∵an+12=an2+
,则an+12-an2=
,
于是有:
+
+…+
=an+12-a12=an+12-1
要证明:
(n+1)
-1≤
+
+…+
≤4(n+1)
-1
只需证明:
n
≤an≤2n
(*)
下面使用数学归纳法证明:
n
≤an≤2n
(n≥1,n∈N*)
①在n=1时,a1=1,
<a1<2,则n=1时 (*)式成立.
②假设n=k时,
k
≤ak≤2k
成立,
由
=
+
≤4k
+
=4k
+
要证明:4k
+
≤4(k+1)
,
只需2k+1≤
k
(k+1)
只需(2k+1)3≤8k(k+1)2
只需1≤4k2+2k,而4k2+2k≥1在k≥1时,恒成立,
于是ak+12=
(k+1)
,于是ak+1≤ 2(k+1)
,
又ak+12=ak2+
≥
k
+
,
要证
k
+
≥
(k+1)
只需证:k+2≥k
(k+1)
,
只需证:4k2+11k+8>0,而4k2+11k+8>0在k≥1时恒成立.
于是:
≥
(k+1)
.
因此
(k+1)
≤
≤2(k+1)
得证.
综合①②可知(*)式得证,从而原不等式成立.
(3)证明:要证明:Sn≤
-
,
由(2)可知只需证:
<
-
(n≥2)(**)
下面用分析法证明:(**)式成立.
要使(**)成立,
只需证:(3n-2)
>(3n-1)
即只需证:(3n-2)3n>(3n-1)3(n-1),
只需证:2n>1.
而2n>1在n≥1时显然成立,
故(**)式得证.
于是由(**)式可知有:
+
+…+
≤
-
因此有:Sn=a1+a2+…+an≤1+2(
+
+…+
)=
-
x2+
|
| 1 |
| x |
∴
| x3+1 |
| x |
∴
| (x+1)(x2-x+1) |
| x |
∴
| x+1 |
| x |
故x>0,或x≤-1.
f(x)定义域为:(-∞,-1]∪(0,+∞).
(2)证明:∵an+12=an2+
| 1 |
| an |
| 1 |
| an |
于是有:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
要证明:
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 2 |
| 3 |
只需证明:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
下面使用数学归纳法证明:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
①在n=1时,a1=1,
| 1 |
| 2 |
②假设n=k时,
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
由
| a | 2 k+1 |
| a | 2 k |
| 1 |
| ak |
| 1 |
| 3 |
| 1 | ||||
|
| 2 |
| 3 |
| 2 | ||
k
|
要证明:4k
| 1 |
| 3 |
| 1 | ||||
|
| 2 |
| 3 |
只需2k+1≤
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
只需1≤4k2+2k,而4k2+2k≥1在k≥1时,恒成立,
于是ak+12=
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 3 |
又ak+12=ak2+
| 1 |
| ak |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 | ||
2k
|
要证
| 1 |
| 4 |
| 2 |
| 3 |
| 1 | ||
2k
|
| 1 |
| 4 |
| 2 |
| 3 |
只需证:k+2≥k
| 1 |
| 3 |
| 2 |
| 3 |
只需证:4k2+11k+8>0,而4k2+11k+8>0在k≥1时恒成立.
于是:
| a | 2 k+1 |
| 1 |
| 4 |
| 2 |
| 3 |
因此
| 1 |
| 2 |
| 1 |
| 3 |
| a | 2 k+1 |
| 1 |
| 3 |
综合①②可知(*)式得证,从而原不等式成立.
(3)证明:要证明:Sn≤
(3n+2)
| |||
| 2 |
| 3 |
| 2 |
由(2)可知只需证:
| 3 | n |
(3n+2)
| |||
| 4 |
[3(n-1)+2]
| |||
| 4 |
下面用分析法证明:(**)式成立.
要使(**)成立,
只需证:(3n-2)
| 3 | n |
| 3 | n-1 |
即只需证:(3n-2)3n>(3n-1)3(n-1),
只需证:2n>1.
而2n>1在n≥1时显然成立,
故(**)式得证.
于是由(**)式可知有:
| 3 | 2 |
| 3 | 3 |
| 3 | n |
(3n+2)
| |||
| 4 |
| 5 |
| 4 |
因此有:Sn=a1+a2+…+an≤1+2(
| 3 | 2 |
| 3 | 3 |
| 3 | n |
(3n+2)
| |||
| 2 |
| 3 |
| 2 |
点评:本题考查数列和不等式的综合运用,解题时要认真审题,注意数学归纳法和分析法在不等式证明中的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
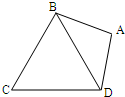 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=