题目内容
在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.(Ⅰ)求证:EF∥平面ACD1;
(Ⅱ)求异面直线EF与AB所成的角的余弦值;
(Ⅲ)在棱BB1上是否存在一点P,使得二面角P-AC-B的大小为30°?若存在,求出BP的长;若不存在,请说明理由.
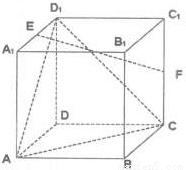
【答案】分析:如图分别以DA、DC、DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系D-xyz,先写出各点坐标:
(I)取AD1中点G,则G(1,0,1),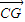 =(1,-2,1),又
=(1,-2,1),又 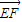 =(-1,2,-1),证明
=(-1,2,-1),证明 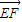 与
与 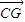 共线即可;
共线即可;
(II)求出两异面直线的方向向量,用数量积公式求夹角余弦即可,易求;
(III)假设存在,设出点P的空间坐标,根据题设中所给的条件二面角P-AC-B的大小为30°利用数量积公式建立关于引入的参数的方程即可,若求得的参数符合题意,则说明存在,否则说明不存在.
解答: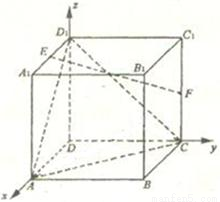 解:如图分别以DA、DC、DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系D-xyz,由已知得D(0,0,0)、A(2,0,0)、B(2,2,0)、
解:如图分别以DA、DC、DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系D-xyz,由已知得D(0,0,0)、A(2,0,0)、B(2,2,0)、
C(0,2,0)、B1(2,2,2)、D1(0,0,2)、E(1,0,2)、F(0,2,1).
(I)取AD1中点G,则G(1,0,1),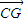 =(1,-2,1),又
=(1,-2,1),又 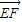 =(-1,2,-1),由
=(-1,2,-1),由 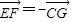 ,
,
∴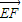 与
与 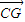 共线.
共线.
从而EF∥CG,
∵CG?平面ACD1,EF?平面ACD1,
∴EF∥平面ACD1.(6分)
(II)∵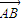 =(0,2,0)∴
=(0,2,0)∴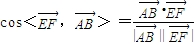 =
=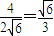
(III)假设满足条件的点P存在,可设点P(2,2,t),(0<t≤2),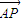 =(0,2,t),
=(0,2,t),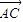 =(-2,2,0)
=(-2,2,0)
平面ACP的一个法向量为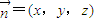 则
则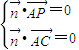 ∴
∴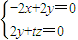 取
取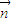 =(1,1,
=(1,1,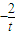 ),易知平面ABC的一个法向量
),易知平面ABC的一个法向量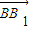 =(0,0,2)依题意知
=(0,0,2)依题意知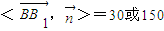 ∴|cos
∴|cos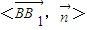 |=
|=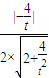 =
=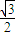 解得t=
解得t=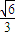 ∈(0,2)∴在棱BB1上存在一点P,当BP的长为
∈(0,2)∴在棱BB1上存在一点P,当BP的长为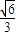 时,二面角P-AC-B的大小为30°
时,二面角P-AC-B的大小为30°
点评:本题考查用向量法证明线面平行,求异面直线所成的角以及二面角,用向量方法解决立体几何中的位置关系、夹角及距离问题是空间向量的一个重要运用,学习时注意总结向量法解立体几何题的规律,此方法也是近几年高考比较热的一个考点.
(I)取AD1中点G,则G(1,0,1),
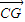 =(1,-2,1),又
=(1,-2,1),又 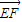 =(-1,2,-1),证明
=(-1,2,-1),证明 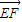 与
与 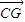 共线即可;
共线即可;(II)求出两异面直线的方向向量,用数量积公式求夹角余弦即可,易求;
(III)假设存在,设出点P的空间坐标,根据题设中所给的条件二面角P-AC-B的大小为30°利用数量积公式建立关于引入的参数的方程即可,若求得的参数符合题意,则说明存在,否则说明不存在.
解答:
 解:如图分别以DA、DC、DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系D-xyz,由已知得D(0,0,0)、A(2,0,0)、B(2,2,0)、
解:如图分别以DA、DC、DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系D-xyz,由已知得D(0,0,0)、A(2,0,0)、B(2,2,0)、C(0,2,0)、B1(2,2,2)、D1(0,0,2)、E(1,0,2)、F(0,2,1).
(I)取AD1中点G,则G(1,0,1),
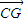 =(1,-2,1),又
=(1,-2,1),又 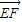 =(-1,2,-1),由
=(-1,2,-1),由 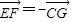 ,
,∴
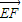 与
与 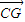 共线.
共线.从而EF∥CG,
∵CG?平面ACD1,EF?平面ACD1,
∴EF∥平面ACD1.(6分)
(II)∵
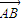 =(0,2,0)∴
=(0,2,0)∴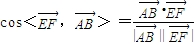 =
=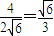
(III)假设满足条件的点P存在,可设点P(2,2,t),(0<t≤2),
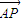 =(0,2,t),
=(0,2,t),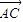 =(-2,2,0)
=(-2,2,0)平面ACP的一个法向量为
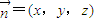 则
则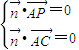 ∴
∴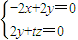 取
取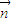 =(1,1,
=(1,1,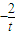 ),易知平面ABC的一个法向量
),易知平面ABC的一个法向量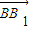 =(0,0,2)依题意知
=(0,0,2)依题意知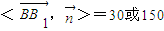 ∴|cos
∴|cos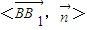 |=
|=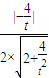 =
=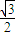 解得t=
解得t=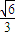 ∈(0,2)∴在棱BB1上存在一点P,当BP的长为
∈(0,2)∴在棱BB1上存在一点P,当BP的长为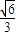 时,二面角P-AC-B的大小为30°
时,二面角P-AC-B的大小为30°点评:本题考查用向量法证明线面平行,求异面直线所成的角以及二面角,用向量方法解决立体几何中的位置关系、夹角及距离问题是空间向量的一个重要运用,学习时注意总结向量法解立体几何题的规律,此方法也是近几年高考比较热的一个考点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在棱长为2的正方体AC1中,G是AA1的中点,则BD到平面GB1D1的距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( ) (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F. (2007•上海)如图,在棱长为2的正方体ABCD-A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小 (结果用反三角函数值表示).
(2007•上海)如图,在棱长为2的正方体ABCD-A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小 (结果用反三角函数值表示).