题目内容
已知函数f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(Ⅰ) 当a=-1时,求f(x)的最大值;
(Ⅱ) 若f(x)在区间(0,e]上的最大值为-3,求a的值;
(Ⅲ) 当a=-1 时,试推断方 是否有实数解.
是否有实数解.
(Ⅰ) 当a=-1时,求f(x)的最大值;
(Ⅱ) 若f(x)在区间(0,e]上的最大值为-3,求a的值;
(Ⅲ) 当a=-1 时,试推断方
 是否有实数解.
是否有实数解.解:(1) 当a=-1时,f(x)=-x+lnx,
f′(x)′=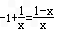
当0<x<1时,f′(x)>0;
当x>1时,f′(x)<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数
f(x)max=f(1)=-1
(2) ∵f′(x)′=a+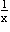 ,x∈(0,e],
,x∈(0,e],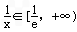
① 若a≥-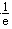 ,则f′′(x)≥0,从而f(x)在(0,e]上增函数
,则f′′(x)≥0,从而f(x)在(0,e]上增函数
∴f(x)max=f(e)=ae+1≥0.不合题意
② 若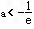 ,则由f′(x)′>0
,则由f′(x)′>0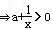 ,
,
即0<x<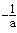
由f(x)<0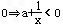 ,即
,即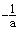 <x≤e.
<x≤e.
从而f(x)在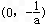 上增函数,在
上增函数,在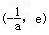 为减函数
为减函数
∴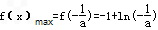
令-1+ln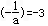 ,则ln
,则ln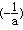 =-2
=-2
∴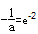 ,即a=
,即a=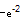 .
.
∵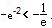
∴a=-e2
(3) 由(1)知当a=-1时f(x)max=f(1)=-1,∴|f(x)|≥1
又令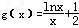 ,
,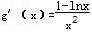
令g′(x)=0,得x=e,
当0<x<e时,g′(x)>0,g(x) 在(0,e)单调递增;
当x>e时,g′(x)<0,g(x) 在(e,+∞)单调递减
∴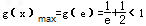
∴g(x)<1
∴|f(x)|>g(x),即|f(x)|>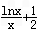
∴方程|f(x)|=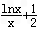 没有实数解.
没有实数解.
f′(x)′=
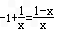
当0<x<1时,f′(x)>0;
当x>1时,f′(x)<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数
f(x)max=f(1)=-1
(2) ∵f′(x)′=a+
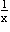 ,x∈(0,e],
,x∈(0,e],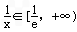
① 若a≥-
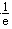 ,则f′′(x)≥0,从而f(x)在(0,e]上增函数
,则f′′(x)≥0,从而f(x)在(0,e]上增函数 ∴f(x)max=f(e)=ae+1≥0.不合题意
② 若
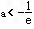 ,则由f′(x)′>0
,则由f′(x)′>0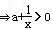 ,
,即0<x<
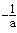
由f(x)<0
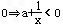 ,即
,即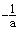 <x≤e.
<x≤e.从而f(x)在
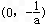 上增函数,在
上增函数,在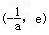 为减函数
为减函数∴
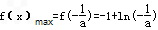
令-1+ln
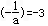 ,则ln
,则ln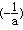 =-2
=-2∴
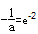 ,即a=
,即a=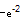 .
.∵
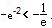
∴a=-e2
(3) 由(1)知当a=-1时f(x)max=f(1)=-1,∴|f(x)|≥1
又令
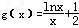 ,
,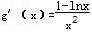
令g′(x)=0,得x=e,
当0<x<e时,g′(x)>0,g(x) 在(0,e)单调递增;
当x>e时,g′(x)<0,g(x) 在(e,+∞)单调递减
∴
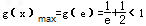
∴g(x)<1
∴|f(x)|>g(x),即|f(x)|>
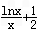
∴方程|f(x)|=
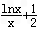 没有实数解.
没有实数解.
练习册系列答案
相关题目