题目内容
已知函数f(x)=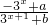 .
.
(1)当a=b=1时,求满足f(x)≥3x的x的取值范围;
(2)若y=f(x)的定义域为R,又是奇函数,求y=f(x)的解析式,判断其在R上的单调性并加以证明.
解:(1)由题意,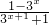 ≥3x,化简得3•(3x)2+2×3x-1≤0…(2分)
≥3x,化简得3•(3x)2+2×3x-1≤0…(2分)
解得-1≤3x≤ …(4分)
…(4分)
所以x≤-1…((6分),如果是其它答案得5分)
(2)已知定义域为R,所以f(0)=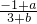 =0?a=1,…(7分)
=0?a=1,…(7分)
又f(1)+f(-1)=0?b=3,…(8分)
所以f(x)=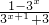 ;…(9分)
;…(9分)
f(x)=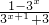 =
= (
(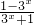 )=
)= (-1+
(-1+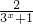 )
)
对任意x1,x2∈R,x1<x2,
可知f(x1)-f(x2)= (
(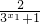 -
- )=-
)=- (
(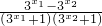 )…(12分)
)…(12分)
因为x1<x2,所以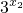 -
-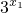 >0,所以f(x1)>f(x2),
>0,所以f(x1)>f(x2),
因此f(x)在R上递减.…(14分)
分析:(1)由题意可得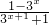 ≥3x从中解得-1≤3x≤
≥3x从中解得-1≤3x≤ ,解此指数不等式即可求得x的取值范围;
,解此指数不等式即可求得x的取值范围;
(2)由f(0)=0,可求得a,f(1)+f(-1)=0可求得b,从而可得y=f(x)的解析式;利用单调性的定义,对任意x1,x2∈R,x1<x2,再作差f(x1)-f(x2),最后判断符号即可.
点评:本题考查指数不等式的解法,考查函数奇偶性的应用,考查函数单调性的判断与证明,属于综合题,难度大,运算量大,属于难题.
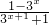 ≥3x,化简得3•(3x)2+2×3x-1≤0…(2分)
≥3x,化简得3•(3x)2+2×3x-1≤0…(2分)解得-1≤3x≤
 …(4分)
…(4分)所以x≤-1…((6分),如果是其它答案得5分)
(2)已知定义域为R,所以f(0)=
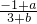 =0?a=1,…(7分)
=0?a=1,…(7分)又f(1)+f(-1)=0?b=3,…(8分)
所以f(x)=
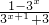 ;…(9分)
;…(9分)f(x)=
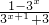 =
= (
(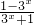 )=
)= (-1+
(-1+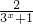 )
)对任意x1,x2∈R,x1<x2,
可知f(x1)-f(x2)=
 (
(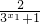 -
- )=-
)=- (
(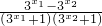 )…(12分)
)…(12分)因为x1<x2,所以
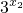 -
-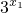 >0,所以f(x1)>f(x2),
>0,所以f(x1)>f(x2),因此f(x)在R上递减.…(14分)
分析:(1)由题意可得
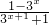 ≥3x从中解得-1≤3x≤
≥3x从中解得-1≤3x≤ ,解此指数不等式即可求得x的取值范围;
,解此指数不等式即可求得x的取值范围;(2)由f(0)=0,可求得a,f(1)+f(-1)=0可求得b,从而可得y=f(x)的解析式;利用单调性的定义,对任意x1,x2∈R,x1<x2,再作差f(x1)-f(x2),最后判断符号即可.
点评:本题考查指数不等式的解法,考查函数奇偶性的应用,考查函数单调性的判断与证明,属于综合题,难度大,运算量大,属于难题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|