题目内容
在正方体
ABCD－A1B1C1D1中，E，F，G，H，M，N分别是正方体的棱A1A，AB，BC，CC1，C1D1，D1A1的中点，试证：E，F，G，H，M，N六点共面．
答案：
解析：
解析：
|
解析： ∵EN∥MF，∴EN与MF共面 ，(2分)又∵EF∥MH，∴EF和MH共面 ．(4分)∵不共线的三点E，F，M确定一个平面，(6分)∴平面与重合，∴点H ．(8分)同理点G．(10分)故E，F，G，H，M，N六点共面．
|
练习册系列答案
优生乐园系列答案
相关题目
在正方体ABCD-A1B1C1D1中，E是棱A1B1的中点，则A1B与D1E所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在正方体ABCD-A1B1C1D1中，AB与平面A1BC1所成角的正弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（本小题满分12分）
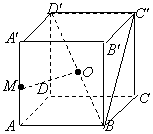
在正方体ABCD－A′B′C′D′中，点M是棱AA′的中点，点O是对角线BD′的中点.
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；
（Ⅱ）求二面角M－BC′－B′的大小；
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；