题目内容
已知抛物线 ,圆
,圆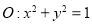 .
.
(1)若抛物线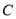 的焦点
的焦点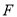 在圆上,且
在圆上,且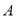 为
为 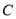 和圆
和圆 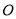 的一个交点,求
的一个交点,求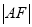 ;
;
(2)若直线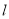 与抛物线
与抛物线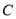 和圆
和圆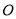 分别相切于点
分别相切于点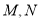 ,求
,求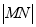 的最小值及相应
的最小值及相应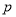 的值.
的值.
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
题目内容
已知抛物线 ,圆
,圆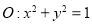 .
.
(1)若抛物线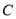 的焦点
的焦点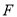 在圆上,且
在圆上,且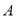 为
为 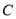 和圆
和圆 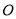 的一个交点,求
的一个交点,求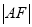 ;
;
(2)若直线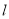 与抛物线
与抛物线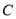 和圆
和圆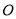 分别相切于点
分别相切于点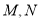 ,求
,求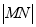 的最小值及相应
的最小值及相应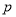 的值.
的值.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案