题目内容
(本小题满分8分)如图5,在四棱锥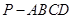 中,底面
中,底面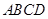 为正方形,
为正方形,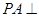 平面
平面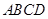 ,
,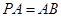 ,点
,点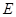 是
是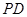 的中点.(1)求证:
的中点.(1)求证: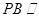 平面
平面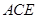 ;
;
(2)若四面体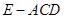 的体积为
的体积为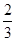 ,求
,求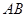 的长.
的长.

【答案】
见解析。
【解析】本小题主要考查直线与平面的位置关系、体积等基础知识,考查空间想象能力、推理论证能力和运算求解能力.
已知点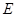 是
是 的中点通常再找一中点构成中位线,得到平行关系。
的中点通常再找一中点构成中位线,得到平行关系。
因为点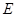 是
是 的中点,所以
的中点,所以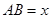 ,则
,则 ,且
,且
,用体积公式列出关于x的等式即可。
(1)证明:连接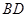 交
交 于点
于点 ,连接
,连接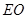 ,
,
因为 是正方形,所以点
是正方形,所以点 是
是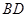 的中点.
的中点.
因为点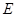 是
是 的中点,
的中点,
所以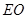 是△
是△ 的中位线.
的中位线.
所以 .
.

因为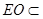 平面
平面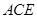 ,
, 平面
平面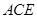 ,
,
所以 平面
平面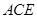 .
.
(2)解:取 的中点
的中点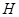 ,连接
,连接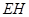 ,
,
因为点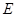 是
是 的中点,所以
的中点,所以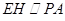 .
.
因为 平面
平面 ,所以
,所以 平面
平面 .
.
设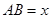 ,则
,则 ,且
,且 .
.
所以
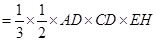
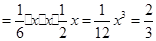 .
.
解得 .
.
故 的长为2.
的长为2.

练习册系列答案
相关题目
 为梯形,
为梯形, ,
, ,求图中阴影部分绕
,求图中阴影部分绕 旋转一周所形成的几何体的表面积和体积。
旋转一周所形成的几何体的表面积和体积。
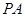 切⊙O于点
切⊙O于点 为
为 引割线交⊙O于
引割线交⊙O于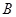 、
、 两点.求证:
两点.求证: .
.
 的棱长是2,
的棱长是2,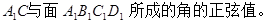

 ,点E是斜边AB上的动点,过E点做矩形EFCG,设矩形EFCG面积为S,矩形一边EF长为
,点E是斜边AB上的动点,过E点做矩形EFCG,设矩形EFCG面积为S,矩形一边EF长为 ,
,
 .求点A到平面PBC的距离.
.求点A到平面PBC的距离.