题目内容
在△ABC中，AC=2，BC=1，cosC=
．
（Ⅰ）求边AB的长；
（Ⅱ）求sin（2A+C）的值．
| 4 |
| 5 |
（Ⅰ）求边AB的长；
（Ⅱ）求sin（2A+C）的值．
（Ⅰ）在△ABC中，AC=2，BC=1，cosC=
，利用余弦定理可得AB2=4+1-2×2×1×
=
∴AB=
（Ⅱ）利用余弦定理可得，cosA=
，∴sinA=
∴sin2A=
，cos2A=
∴sin（2A+C）=sin2AcosC+cos2AsinC=
×
+
×
=1．
| 4 |
| 5 |
| 4 |
| 5 |
| 9 |
| 5 |
∴AB=
| 3 |
| 5 |
| 5 |
（Ⅱ）利用余弦定理可得，cosA=
| 2 |
| 5 |
| 5 |
| ||
| 5 |
∴sin2A=
| 4 |
| 5 |
| 3 |
| 5 |
∴sin（2A+C）=sin2AcosC+cos2AsinC=
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
练习册系列答案
相关题目
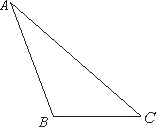如图，在△ABC中，AC=2，BC=1，
如图，在△ABC中，AC=BC，AB=2，O为AB的中点，沿OC将△AOC折起到△A′OC的位置，使得直线A′B与平面ABC成30°角．