题目内容
 如图,在△ABC中,AC=BC,AB=2,O为AB的中点,沿OC将△AOC折起到△A′OC的位置,使得直线A′B与平面ABC成30°角.
如图,在△ABC中,AC=BC,AB=2,O为AB的中点,沿OC将△AOC折起到△A′OC的位置,使得直线A′B与平面ABC成30°角.(1)若点A′到直线BC的距离为l,求二面角A′-BC-A的大小;
(2)若∠A′CB+∠OCB=π,求BC边的长.
分析:(1)过点A′作A′D⊥AB,垂足为D,由已知中AC=BC,沿OC将△AOC折起到△A′OC的位置,易根据面面垂直的判定定理得到平面A′OB⊥平面ABC,进而得到A′D⊥平面ABC,再根据已知中直线A′B与平面ABC成30°角,求出A′D的长度,过点D作DE⊥BC,垂足为E,连接A′E,易得∠A′ED为二面角A′-BC-A的平面角,解Rt△A′DE即可求出二面角A′-BC-A的大小;
(2)设BC=x,∠A′CB=θ,则A′C=x,∠OCB=π-θ,解Rt△BOC,△A′DB,△A′BC,可以求出x值的大小,进而得到BC边的长.
(2)设BC=x,∠A′CB=θ,则A′C=x,∠OCB=π-θ,解Rt△BOC,△A′DB,△A′BC,可以求出x值的大小,进而得到BC边的长.
解答: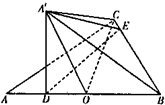 解:(1)由已知,OC⊥OB,OC⊥OA′从而平面A′OB⊥平面ABC.
解:(1)由已知,OC⊥OB,OC⊥OA′从而平面A′OB⊥平面ABC.
过点A′作A′D⊥AB,垂足为D,则A′D⊥平面ABC,…(2分)
∴∠A′ED=30°,又A′O=BO=1,∴∠A′OD=60°,
从而A′D=A′O•sin60°=
.…(4分)
过点D作DE⊥BC,垂足为E,连接A′E,据三垂线定理,A′E⊥BC.
∴∠A′ED为二面角A′-BC-A的平面角.…(5分)
由已知,A′E=1,在Rt△A′DE中sin∠A′ED=
=
∴∠A′ED=60°故二面角A′-BC-A的大小为60°.…(6分)
(2)设BC=x,∠A′CB=θ,则A′C=x,∠OCB=π-θ.
在Rt△BOC中,sin∠OCB=
∴sin(π-θ)=
,即sinθ=
…(9分)
在△A′DB中,A′B=
=
在△A′BC中,A′B2=A′C2+BC2-2A′C•BC•cos∠A′CB
∴3=x2+x2-2x2•cosθ,即cosθ=1-
…(12分)
∵sin2θ+cos2θ=1
∴
+(1-
)2=1
解得x=
故BC=
…(14分)
 解:(1)由已知,OC⊥OB,OC⊥OA′从而平面A′OB⊥平面ABC.
解:(1)由已知,OC⊥OB,OC⊥OA′从而平面A′OB⊥平面ABC.过点A′作A′D⊥AB,垂足为D,则A′D⊥平面ABC,…(2分)
∴∠A′ED=30°,又A′O=BO=1,∴∠A′OD=60°,
从而A′D=A′O•sin60°=
| ||
| 2 |
过点D作DE⊥BC,垂足为E,连接A′E,据三垂线定理,A′E⊥BC.
∴∠A′ED为二面角A′-BC-A的平面角.…(5分)
由已知,A′E=1,在Rt△A′DE中sin∠A′ED=
| A′D |
| A′E |
| ||
| 2 |
∴∠A′ED=60°故二面角A′-BC-A的大小为60°.…(6分)
(2)设BC=x,∠A′CB=θ,则A′C=x,∠OCB=π-θ.
在Rt△BOC中,sin∠OCB=
| OB |
| BC |
∴sin(π-θ)=
| 1 |
| x |
| 1 |
| x |
在△A′DB中,A′B=
| A′D |
| sin30° |
| 3 |
在△A′BC中,A′B2=A′C2+BC2-2A′C•BC•cos∠A′CB
∴3=x2+x2-2x2•cosθ,即cosθ=1-
| 3 |
| 2x2 |
∵sin2θ+cos2θ=1
∴
| 1 |
| x2 |
| 3 |
| 2x2 |
解得x=
3
| ||
| 4 |
故BC=
3
| ||
| 4 |
点评:本题考查的知识点是二面角的平面角及求法,空间两点之间的距离计算,其中(1)的关键是构造出∠A′ED为二面角A′-BC-A的平面角,(2)的关键是设出BC边的长,根据已知条件,结合解三角形的方法(余弦定理)构造出关于x的方程.

练习册系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知