题目内容
已知函数f(x)= x3+x2-2。
x3+x2-2。
(1)设{an}是正数组成的数列,前n项和为Sn,其中a1=3。若点(an,an+12-2an+1)(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(2)求函数f(x)在区间(a-1,a)内的极值。
 x3+x2-2。
x3+x2-2。(1)设{an}是正数组成的数列,前n项和为Sn,其中a1=3。若点(an,an+12-2an+1)(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(2)求函数f(x)在区间(a-1,a)内的极值。
解:(1)因为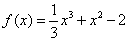
所以
由点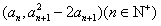 在函数y=f′(x)的图象上
在函数y=f′(x)的图象上
又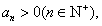
所以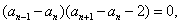
所以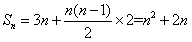
又因为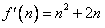
所以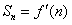
故点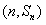 也在函数y=f′(x)的图象上;
也在函数y=f′(x)的图象上;
(2)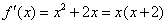
由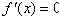 得
得
当x变化时,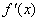 ,
, 的变化情况如下表:
的变化情况如下表:

注意到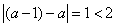 ,从而
,从而
①当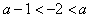 ,即
,即 时,f(x)的极大值为
时,f(x)的极大值为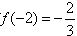
此时f(x)无极小值;
②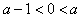 ,即
,即 时,f(x)的极小值为f(0)=-2,此时f(x)无极大值;
时,f(x)的极小值为f(0)=-2,此时f(x)无极大值;
③当a≤-2或-1≤a≤0或a≥1时,f(x)既无极大值又无极小值。
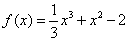
所以

由点
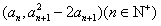 在函数y=f′(x)的图象上
在函数y=f′(x)的图象上又
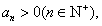
所以
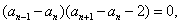
所以
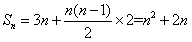
又因为
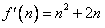
所以
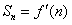
故点
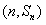 也在函数y=f′(x)的图象上;
也在函数y=f′(x)的图象上;(2)
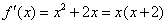
由
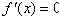 得
得
当x变化时,
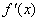 ,
, 的变化情况如下表:
的变化情况如下表:
注意到
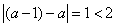 ,从而
,从而①当
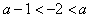 ,即
,即 时,f(x)的极大值为
时,f(x)的极大值为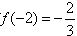
此时f(x)无极小值;
②
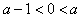 ,即
,即 时,f(x)的极小值为f(0)=-2,此时f(x)无极大值;
时,f(x)的极小值为f(0)=-2,此时f(x)无极大值;③当a≤-2或-1≤a≤0或a≥1时,f(x)既无极大值又无极小值。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|