题目内容
设函数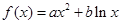 ,其中
,其中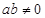 .证明:当
.证明:当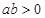 时,函数
时,函数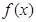 没有极值点;当
没有极值点;当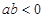 时,函数
时,函数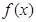 有且只有一个极值点,并求出极值.
有且只有一个极值点,并求出极值.
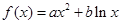 ,其中
,其中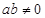 .证明:当
.证明:当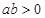 时,函数
时,函数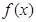 没有极值点;当
没有极值点;当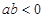 时,函数
时,函数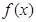 有且只有一个极值点,并求出极值.
有且只有一个极值点,并求出极值.当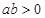 时,函数
时,函数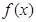 没有极值点;
没有极值点;
当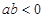 时,
时,
若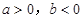 时,函数
时,函数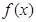 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为 .
.
若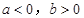 时,函数
时,函数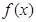 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为 .
.
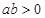 时,函数
时,函数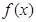 没有极值点;
没有极值点;当
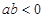 时,
时,若
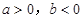 时,函数
时,函数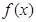 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为 .
.若
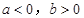 时,函数
时,函数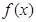 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为 .
.试题分析:证明:因为
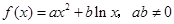 ,所以
,所以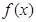 的定义域为
的定义域为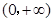 .
.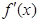
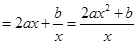 .
.当
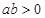 时,如果
时,如果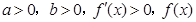 在
在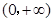 上单调递增;
上单调递增;如果
 在
在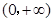 上单调递减.
上单调递减.所以当
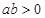 ,函数
,函数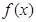 没有极值点.
没有极值点.当
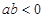 时,
时,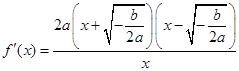
令
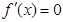 ,得
,得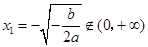 (舍去),
(舍去),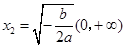 ,
,当
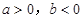 时,
时,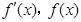 随
随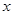 的变化情况如下表:
的变化情况如下表: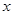 |  | 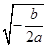 | 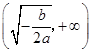 |
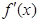 | 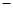 | 0 | 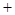 |
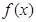 | 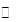 | 极小值 | 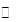 |
函数
 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为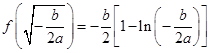 .
.当
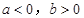 时,
时,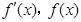 随
随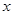 的变化情况如下表:
的变化情况如下表: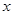 |  | 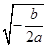 | 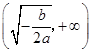 |
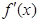 |  | 0 | 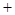 |
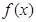 | 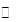 | 极大值 | 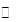 |
函数
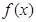 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为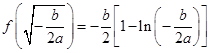 .
.综上所述,当
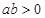 时,函数
时,函数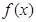 没有极值点;
没有极值点;当
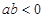 时,
时,若
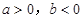 时,函数
时,函数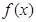 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为 .
.若
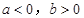 时,函数
时,函数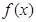 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为 .
.点评:解决的关键是能对于含有参数的函数的导数的符号进行分类讨论,得到结论,属于中档题。

练习册系列答案
相关题目
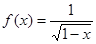 的定义域是
的定义域是 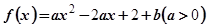 在区间
在区间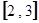 上的值域为
上的值域为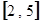
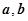 的值;
的值;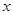 的函数
的函数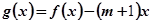 在区间
在区间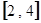 上为单调函数,求实数
上为单调函数,求实数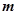 的取值范围.
的取值范围. 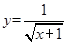 的定义域是( )
的定义域是( )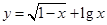 的定义域为 .
的定义域为 .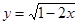 的定义域为集合A,函数
的定义域为集合A,函数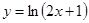 的定义域为B,则
的定义域为B,则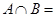
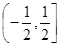
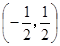
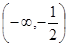
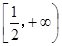
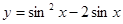 的值域是
的值域是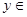 ;
;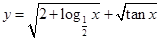 的定义域是( )
的定义域是( )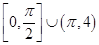
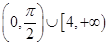
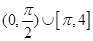
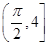
 是坐标原点,且
是坐标原点,且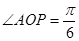 ,
, .
.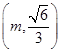 ,求
,求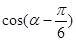 的值;
的值; ,求
,求 的值域.
的值域.