题目内容
【题目】为了解某校高三毕业班报考体育专业学生的体重(单位:千克)情况,将从该市某学校抽取的样本数据整理后得到如下频率分布直方图.已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12. (I)求该校报考体育专业学生的总人数n;
(Ⅱ)若用这所学校的样本数据来估计该市的总体情况,现从该市报考体育专业的学生中任选3人,设ξ表示体重超过60千克的学生人数,求ξ的分布列和数学期望.
【答案】解:(I)设该校报考体育专业的人数为n,前三小组的频率分别为p1 , p2 , p3 , 则由题意可知, 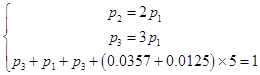 ,
,
解得p1=0.125,p2=0.25,p3=0.375.
又因为p2=0.25= ![]() ,故n=48.
,故n=48.
(II)由(I)可得,一个报考学生体重超过60公斤的概率为p=p3+(0.0375+0.0125)×5= ![]() .
.
所以ξ服从二项分布,P(ξ=k)=C ![]() (
( ![]() )k(
)k( ![]() )2﹣k , k=0,1,2,3
)2﹣k , k=0,1,2,3
∴随机变量ξ的分布列为:
则Eξ=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =
= ![]() .(或Eξ=3×
.(或Eξ=3× ![]() =
= ![]() )
)
【解析】(I)设报考体育专业的人数为n,前三小组的频率分别为p1 , p2 , p3 , 根据前3个小组的频率之比为1:2:3和所求频率和为1建立方程组,解之即可求出第二组频率,然后根据样本容量等于 ![]() 进行求解即可;(II)由(I)可得,一个报考学生体重超过60公斤的概率为p,通过X服从二项分布P(ξ=k),从而求出ξ的分布列,最后利用数学期望公式进行求解.
进行求解即可;(II)由(I)可得,一个报考学生体重超过60公斤的概率为p,通过X服从二项分布P(ξ=k),从而求出ξ的分布列,最后利用数学期望公式进行求解.
【考点精析】利用离散型随机变量及其分布列对题目进行判断即可得到答案,需要熟知在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案