题目内容
【题目】已知![]()
(1)证明函数f ( x )的图象关于![]() 轴对称;
轴对称;
(2)判断![]() 在
在![]() 上的单调性,并用定义加以证明;
上的单调性,并用定义加以证明;
(3)当x∈[1,2]时函数f (x )的最大值为![]() ,求此时a的值。
,求此时a的值。
【答案】(1)证明见解析;(2)答案见解析;(3) ![]() ,或
,或![]()
【解析】试题分析:(1)定义域为![]() ,证明
,证明![]() ,确定函数为偶函数,从而证得函数
,确定函数为偶函数,从而证得函数![]() 的图象关于
的图象关于![]() 轴对称;(2)利用单调性的定义,设
轴对称;(2)利用单调性的定义,设![]() ,作差
,作差![]() ,化简确定差的正负,从而证得函数的单调性;(3)根据(2)的结论,利用函数的单调性,即可得到函数的最大值,再根据函数的最大值为
,化简确定差的正负,从而证得函数的单调性;(3)根据(2)的结论,利用函数的单调性,即可得到函数的最大值,再根据函数的最大值为![]() ,列出等式,即可求得
,列出等式,即可求得![]() 的值.
的值.
试题解析:(1)要证明函数![]() 的图象关于
的图象关于![]() 轴对称,只须证明函数
轴对称,只须证明函数![]() 是偶函数
是偶函数
∵![]() ,由
,由![]()
∴函数![]() 是偶函数,即函数
是偶函数,即函数![]() 的图象关于
的图象关于![]() 轴对称
轴对称
(2).证明:任取![]() 且
且![]() ,因为
,因为
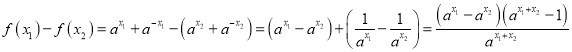 ,
,
①当![]() 时,由0<
时,由0<![]() ,则
,则![]() ,则
,则![]() .
.![]() .
.![]() .
.![]() ;
;
![]() <0即
<0即![]() ;
;
②当![]() 时,由0<
时,由0<![]() ,则x1+x2>0,则
,则x1+x2>0,则![]() .
.![]() .
.![]() .
.![]() ;
; ![]() 即
即![]() ;
;
所以,对于任意![]() (
(![]() ),f(x)在
),f(x)在![]() 上都为增函数。
上都为增函数。
(3)由(2)知![]() 在
在![]() 上为增函数,则当
上为增函数,则当![]() 时,函数
时,函数![]() 亦为增函数;
亦为增函数;
由于函数![]() 的最大值为
的最大值为![]() ,则
,则![]() ,即
,即![]() ,解得
,解得![]() ,或
,或![]()

练习册系列答案
相关题目