题目内容
已知双曲线![]() 的左右两个焦点分别为
的左右两个焦点分别为![]() ,点P在双曲线右支上.
,点P在双曲线右支上.
(Ⅰ)若当点P的坐标为![]() 时,
时,![]() ,求双曲线的方程;
,求双曲线的方程;
(Ⅱ)若![]() ,求双曲线离心率
,求双曲线离心率![]() 的最值,并写出此时双曲线的渐进线方程.
的最值,并写出此时双曲线的渐进线方程.
(Ⅰ)所求双曲线的方程为: ![]()
(Ⅱ)双曲线的渐进线方程为![]()
解析:
(Ⅰ)(法一)由题意知,![]()
![]() ,
, ![]()
![]() ,
,
![]()
![]() ,
,![]()
![]()
![]() (1分)
(1分)
解得 ![]() . 由双曲线定义得:
. 由双曲线定义得: ![]()
![]()
![]() ,
,![]()
![]() 所求双曲线的方程为:
所求双曲线的方程为: ![]()
(法二) 因![]() ,由斜率之积为
,由斜率之积为![]() ,可得解.
,可得解.
(Ⅱ)设![]() ,
,
(法一)设P的坐标为![]() , 由焦半径公式得
, 由焦半径公式得![]() ,
,![]() ,
,![]()
![]() ,
,
![]() 的最大值为2,无最小值. 此时
的最大值为2,无最小值. 此时![]() ,
,
![]() 此时双曲线的渐进线方程为
此时双曲线的渐进线方程为![]()
(法二)设![]() ,
,![]() .
.
(1)当![]() 时,
时, ![]() ,
, ![]()
此时 ![]() .
.
(2)当![]() ,由余弦定理得:
,由余弦定理得:
![]()
![]()
![]() ,
,
![]() ,
,![]() ,综上,
,综上,![]() 的最大值为2,但
的最大值为2,但![]() 无最小值. (以下法一)
无最小值. (以下法一)

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 的左右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线l与双曲线C相交,其中一个交点为
的左右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线l与双曲线C相交,其中一个交点为 .
. 的左右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线l与双曲线C相交,其中一个交点为
的左右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线l与双曲线C相交,其中一个交点为 .
.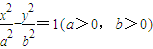 的左右两个焦点分别是F1,F2,P是它左支上的一点,P到左准线的距离为d.
的左右两个焦点分别是F1,F2,P是它左支上的一点,P到左准线的距离为d. x是已知双曲线的一条渐近线,是否存在P点,使d,|PF1|,|PF2|成等比数列?若存在,写出P点坐标,若不存在,说明理由;
x是已知双曲线的一条渐近线,是否存在P点,使d,|PF1|,|PF2|成等比数列?若存在,写出P点坐标,若不存在,说明理由;