题目内容
已知双曲线
的左右两个焦点分别为F1，F2．过右焦点F2且与x轴垂直的直线l与双曲线C相交，其中一个交点为
．（1）求双曲线C的方程；（2）设双曲线C的虚轴一个端点为B（0，-b），求△F1BM的面积．
【答案】分析：（1）由条件可知
，|MF2|=1，|MF1|=3，根据双曲线的定义得2a=|MF1|-|MF2|=3-1=2，由此可求出双曲线方程．
（2）由题意知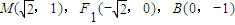
，直线MF1的方程是
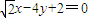，点B到直线MF1的距离
，|MF1|=3，由此能求出△F1BM的面积．
解答：解：（1）由条件可知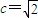
，|MF2|=1，
在直角△F1F2M中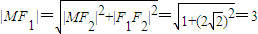
，
根据双曲线的定义得2a=|MF1|-|MF2|=3-1=2，a=1，从而b=1，
所以双曲线方程为x2-y2=1．
（2）由题意知
，直线MF1的方程是
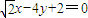（10分）
点B到直线MF1的距离
，
又|MF1|=3，所以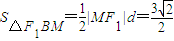
．
点评：本题考查圆锥曲线的综合运用，解题时要注意公式的灵活运用．
，|MF2|=1，|MF1|=3，根据双曲线的定义得2a=|MF1|-|MF2|=3-1=2，由此可求出双曲线方程．（2）由题意知
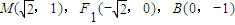，直线MF1的方程是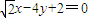，点B到直线MF1的距离，|MF1|=3，由此能求出△F1BM的面积．解答：解：（1）由条件可知
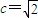，|MF2|=1，在直角△F1F2M中
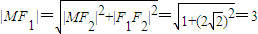，根据双曲线的定义得2a=|MF1|-|MF2|=3-1=2，a=1，从而b=1，
所以双曲线方程为x2-y2=1．
（2）由题意知
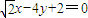，直线MF1的方程是（10分）点B到直线MF1的距离
，又|MF1|=3，所以
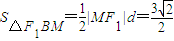．点评：本题考查圆锥曲线的综合运用，解题时要注意公式的灵活运用．
练习册系列答案
相关题目
的左右两个焦点分别为F1，F2．过右焦点F2且与x轴垂直的直线l与双曲线C相交，其中一个交点为
．
的左右两个焦点分别为
,点P在双曲线右支上.
时,
,求双曲线的方程；
,求双曲线离心率
的最值,并写出此时双曲线的渐进线方程.
的左右两个焦点分别为F1，F2．过右焦点F2且与x轴垂直的直线l与双曲线C相交，其中一个交点为
．
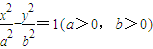的左右两个焦点分别是F1，F2，P是它左支上的一点，P到左准线的距离为d．
x是已知双曲线的一条渐近线，是否存在P点，使d，|PF1|，|PF2|成等比数列？若存在，写出P点坐标，若不存在，说明理由；