题目内容
已知双曲线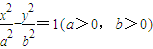 的左右两个焦点分别是F1,F2,P是它左支上的一点,P到左准线的距离为d.
的左右两个焦点分别是F1,F2,P是它左支上的一点,P到左准线的距离为d.(1)若y=
 x是已知双曲线的一条渐近线,是否存在P点,使d,|PF1|,|PF2|成等比数列?若存在,写出P点坐标,若不存在,说明理由;
x是已知双曲线的一条渐近线,是否存在P点,使d,|PF1|,|PF2|成等比数列?若存在,写出P点坐标,若不存在,说明理由;(2)在已知双曲线的左支上,使d,|PF1|,|PF2|成等比数列的P点存在时,求离心率e的取值范围.
【答案】分析:(1)假设存在点P(x,y)满足题中条件,根据渐近线方程求得a和b的关系,进而求得a和c的关系求得e;进而根据 求得|PF2|=2|PF1|,求得准线方程,表示出|PF1|和|PF2|,根据双曲线的定义可知|PF1|=-(a+ex),|PF2|=a-ex,进而求得x,代入双曲线方程求得y,则P点坐标可得.
求得|PF2|=2|PF1|,求得准线方程,表示出|PF1|和|PF2|,根据双曲线的定义可知|PF1|=-(a+ex),|PF2|=a-ex,进而求得x,代入双曲线方程求得y,则P点坐标可得.
(2)根据双曲线的定义可知|PF1|=ed,|PF2|=|PF1|+2a=ed+2a,进而根据d,|PF1|,|PF2|成等比数列推断(ed)2=ed2+2ad,将e= 和P的坐标代入根据x1≤-a,求得 a2+2ac-c2≥0整理后可求得离心率e的范围.
和P的坐标代入根据x1≤-a,求得 a2+2ac-c2≥0整理后可求得离心率e的范围.
解答:解:(1)假设存在点P(x,y)满足题中条件.
∵双曲线的一条渐近线为y= x,∴
x,∴ =
= ,b=
,b=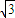 a,∴b2=3a2,c2-a2=3a2,e=
a,∴b2=3a2,c2-a2=3a2,e=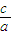 =2.
=2.
由 =2得,
=2得,
|PF2|=2|PF1|①
∵双曲线的两准线方程为x=±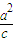 ,
,
∴|PF1|=|2x+2 |=|2x+a|,|PF2|=|2x-
|=|2x+a|,|PF2|=|2x- |=|2x-a|.
|=|2x-a|.
∵点P在双曲线的左支上,
∴|PF1|=-(a+ex),|PF2|=a-ex,代入①得:a-ex=-2(a+ex),
∴x=-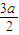 ,代入双曲线方程得y=±
,代入双曲线方程得y=± .
.
∴存在点P使d、|PF1|、|PF2|成等比数列,点P的坐标是(- ,±
,±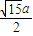 ).
).
(2)|PF1|=ed,
∵d,|PF1|,|PF2|成等比数列
∴(ed)2=ed2+2ad 由(1)得x1= ,将e=
,将e=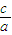 和P的坐标代入..
和P的坐标代入..
因为x1≤-a.整理可得 a2+2ac-c2≥0
两边同除c2.得e2-2e-1≤0.所以1- <e<
<e<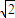 +1
+1
∵e>1
∴e∈(1,1+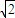 )
)
点评:本题主要考查了双曲线的应用.考查了学生综合分析问题的能力.
 求得|PF2|=2|PF1|,求得准线方程,表示出|PF1|和|PF2|,根据双曲线的定义可知|PF1|=-(a+ex),|PF2|=a-ex,进而求得x,代入双曲线方程求得y,则P点坐标可得.
求得|PF2|=2|PF1|,求得准线方程,表示出|PF1|和|PF2|,根据双曲线的定义可知|PF1|=-(a+ex),|PF2|=a-ex,进而求得x,代入双曲线方程求得y,则P点坐标可得.(2)根据双曲线的定义可知|PF1|=ed,|PF2|=|PF1|+2a=ed+2a,进而根据d,|PF1|,|PF2|成等比数列推断(ed)2=ed2+2ad,将e=
 和P的坐标代入根据x1≤-a,求得 a2+2ac-c2≥0整理后可求得离心率e的范围.
和P的坐标代入根据x1≤-a,求得 a2+2ac-c2≥0整理后可求得离心率e的范围.解答:解:(1)假设存在点P(x,y)满足题中条件.
∵双曲线的一条渐近线为y=
 x,∴
x,∴ =
= ,b=
,b=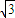 a,∴b2=3a2,c2-a2=3a2,e=
a,∴b2=3a2,c2-a2=3a2,e=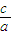 =2.
=2.由
 =2得,
=2得,|PF2|=2|PF1|①
∵双曲线的两准线方程为x=±
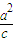 ,
,∴|PF1|=|2x+2
 |=|2x+a|,|PF2|=|2x-
|=|2x+a|,|PF2|=|2x- |=|2x-a|.
|=|2x-a|.∵点P在双曲线的左支上,
∴|PF1|=-(a+ex),|PF2|=a-ex,代入①得:a-ex=-2(a+ex),
∴x=-
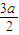 ,代入双曲线方程得y=±
,代入双曲线方程得y=± .
.∴存在点P使d、|PF1|、|PF2|成等比数列,点P的坐标是(-
 ,±
,±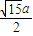 ).
).(2)|PF1|=ed,
∵d,|PF1|,|PF2|成等比数列
∴(ed)2=ed2+2ad 由(1)得x1=
 ,将e=
,将e=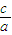 和P的坐标代入..
和P的坐标代入..因为x1≤-a.整理可得 a2+2ac-c2≥0
两边同除c2.得e2-2e-1≤0.所以1-
 <e<
<e<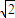 +1
+1∵e>1
∴e∈(1,1+
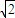 )
)点评:本题主要考查了双曲线的应用.考查了学生综合分析问题的能力.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 的左右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线l与双曲线C相交,其中一个交点为
的左右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线l与双曲线C相交,其中一个交点为 .
. 的左右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线l与双曲线C相交,其中一个交点为
的左右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线l与双曲线C相交,其中一个交点为 .
.