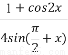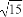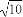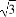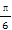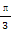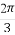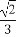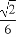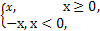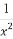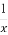Question

已知数列{an}满足:a1=m(m为正整数),an+1=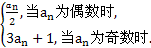若a6=1,则m所有可能的值为　　　.

 

Answer 1

4或5或32

【解析】根据递推式以及a1=m(m为正整数)可知数列{an}中的项都是正整数.

a6=1,若a6=,则a5=2,若a6=3a5+1,则a5=0,故只能是a5=2.

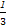若a5=,则a4=4,若a5=3a4+1,则a4=,故只能是a4=4.

若a4=,则a3=8,若a4=3a3+1,则a3=1.

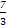(1)当a3=8时,若a3=,则a2=16,若a3=3a2+1,则a2=,故只能是a2=16,若a2=,则a1=32,若a2=3a1+1,则a1=5.

(2)当a3=1时,若a3=,则a2=2,若a3=3a2+1,则a2=0,故只能是a2=2.

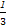若a2=,则a1=4,若a2=3a1+1,则a1=,故只能是a1=4.

综上所述:a1的值,即m的值只能是4或5或32.