题目内容
(本小题满分12分)已知函数 ,
,
(1)若 时,
时, 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围;
(2)设函数 的图象
的图象 与函数
与函数 的图象
的图象 交于
交于 ,
, 两点,过线段
两点,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 、
、 于点
于点 ,
, ,问是否存在点
,问是否存在点 ,使
,使 在
在 处的切线与
处的切线与 在
在 处的切线平行?若存在,求
处的切线平行?若存在,求 的横坐标,若不存在,请说明理由。
的横坐标,若不存在,请说明理由。
【答案】
(1)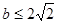 ;(2)点
;(2)点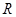 不存在。
不存在。
【解析】
试题分析:(1)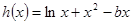 ,
,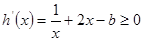 得到
得到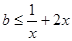 在
在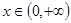 上恒成立,因为
上恒成立,因为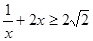 ,所以
,所以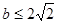 ……
…… …… …… … ……… … ………..4分
……
…… …… …… … ……… … ………..4分
(2)设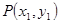 ,
,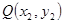 ,则有
,则有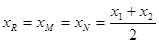 ,令
,令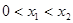
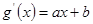 ,假设
,假设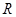 点存在,则
点存在,则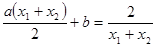 … ……
… … … ……. . 6分
… ……
… … … ……. . 6分
又因为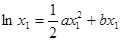 ,
,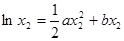 ,得到
,得到
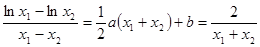 ,即
,即 …… …
……. . 8分
…… …
……. . 8分
令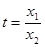 ,设
,设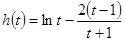 ,
,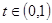 ,
,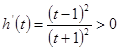 ,得到
,得到
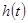 在
在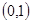 内单调递增,
内单调递增,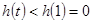 ,假设不成立,所以点
,假设不成立,所以点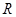 不存在。………..12分
不存在。………..12分
考点:导数的几何意义;利用导数研究函数的单调性。
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,同时考查了转化与划归的思想,分析问题解决问题的能力,属于中档题.

练习册系列答案
相关题目