题目内容
【题目】(1)在边长为1的正方形![]() 内任取一点
内任取一点![]() ,求事件“
,求事件“![]() ”的概率;(2)某班在一次数学活动中,老师让全班56名同学每人随机写下一对都小于1的正实数
”的概率;(2)某班在一次数学活动中,老师让全班56名同学每人随机写下一对都小于1的正实数![]() 、
、![]() ,统计出两数能与1构成锐角三角形的三边长的数对
,统计出两数能与1构成锐角三角形的三边长的数对![]() 共有12对,请据此估计
共有12对,请据此估计![]() 的近似值(精确到
的近似值(精确到![]() ).
).
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据题意画出满足条件的点![]() 的图形,即可利用几何概型求解相应的概率;(2)以点
的图形,即可利用几何概型求解相应的概率;(2)以点![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立平面直角坐标系,列出事件
轴建立平面直角坐标系,列出事件![]() 满足的条件,利用几何概型的计算公式,即可求解结论.
满足的条件,利用几何概型的计算公式,即可求解结论.
试题解析:(1)如图,在边长为1的正方形![]() 内任取一点
内任取一点![]() ,满足条件的点
,满足条件的点![]() 落在扇形
落在扇形![]() 内(图中阴影部分),由几何概型概率计算公式,有:
内(图中阴影部分),由几何概型概率计算公式,有:![]() ,
,
故事件“![]() ”发生的概率为
”发生的概率为![]() .
.

(2)以点![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立平面直角坐标系,如图所示:任取两个小于1的正数
轴建立平面直角坐标系,如图所示:任取两个小于1的正数![]() ,
,![]() ,所有基本事件构成区域
,所有基本事件构成区域 ,即正方形
,即正方形![]() 内部;
内部;
事件![]() “以
“以![]() ,
,![]() 与1为边长能构成锐角三角形”包含的基本事件构成区域
与1为边长能构成锐角三角形”包含的基本事件构成区域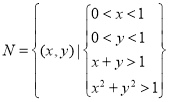 ,即扇形
,即扇形![]() 以外正方形
以外正方形![]() 以内的阴影部分;
以内的阴影部分;
由(1)知:![]() ,
,
全班56名同学每人随机写下一对都小于1的正实数![]() 、
、![]() ,可以看作在区域
,可以看作在区域![]() 中任取56个点;满足“以
中任取56个点;满足“以![]() ,
,![]() 与1为边长能构成锐角三角形”的
与1为边长能构成锐角三角形”的![]() 共有12对,即有12个点落在区域
共有12对,即有12个点落在区域![]() 中,
中,
故其概率为![]() ,用频率估计概率,有
,用频率估计概率,有![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() 的近似值为
的近似值为![]() .
.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目

