题目内容
关于x的三次函数y=f(x)的两个极值点为P、Q,其中P为原点,Q在曲线y=1+
上,则曲线y=f(x)的切线斜率的最大值的最小值为
.
| 2x-x2 |
| 3 |
| 4 |
| 3 |
| 4 |
分析:可以设f(x)=ax3+bx2+cx+d,根据已知条件减少未知量,对其进行求导转化为求f′(x)最大值的表达式,可以利用三角代换,求出a,b关于θ的表达式,再进行代入求得其最小值;
解答:解:设f(x)=ax3+bx2+cx+d,依题意可得,f(0)=0且f′(0)=0,
∴c=d=0,故f(x)=ax3+bx2,
∴f′(x)=3ax2+2bx,由y=1+
及点Q在上面,
可设Q(1+cosθ,1+sinθ),θ∈[0,π],由Q为一个极值点,
得
,
显然cosθ≠1,θ≠π,
∴1+cosθ=-
,
∴
,∵a<0,
∴f′(x)=3ax2+2bx存在最大值:f′(
)=f(-
)=
×
利用数形结合可求得:
×
=
×KOQ,
求出直线OQ斜率的最小值即可:可知Q点在(2,1)处斜率最小:KOQ=
,
∴
×KOQ=
,
曲线y=f(x)的切线斜率的最大值的最小值为
,
故答案为:
;
∴c=d=0,故f(x)=ax3+bx2,
∴f′(x)=3ax2+2bx,由y=1+
| 2x-x2 |
可设Q(1+cosθ,1+sinθ),θ∈[0,π],由Q为一个极值点,
得
|
显然cosθ≠1,θ≠π,
∴1+cosθ=-
| 2b |
| 3a |
∴
|
∴f′(x)=3ax2+2bx存在最大值:f′(
| b |
| 3a |
| 1+cosθ |
| 2 |
| 3 |
| 2 |
| 1+sinθ |
| 1+cosθ |
利用数形结合可求得:
| 3 |
| 2 |
| 1+sinθ |
| 1+cosθ |
| 3 |
| 2 |
求出直线OQ斜率的最小值即可:可知Q点在(2,1)处斜率最小:KOQ=
| 1 |
| 2 |
∴
| 3 |
| 2 |
| 3 |
| 4 |
曲线y=f(x)的切线斜率的最大值的最小值为
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:此题考查了利用导数研究函数的最值问题,比较难想到的是利用三角代换求出函数f′(x)的最大值表达式,此题计算量比较大,考查了学生的计算能力;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
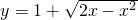 上,则曲线y=f(x)的切线斜率的最大值的最小值为________.
上,则曲线y=f(x)的切线斜率的最大值的最小值为________.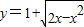 上,则曲线y=f(x)的切线斜率的最大值的最小值为 .
上,则曲线y=f(x)的切线斜率的最大值的最小值为 .