题目内容
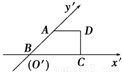
 有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示,∠ABC=45°,AB=2,AD=1,DC⊥BC,则这块菜地的面积为( )
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示,∠ABC=45°,AB=2,AD=1,DC⊥BC,则这块菜地的面积为( )分析:以O点为坐标原点,在直观图中建立平面直角坐标系,按斜二测画直观图的原则,找到四边形ABCD的四个顶点在平面直角坐标系下对应的点,即把直观图中的点还原回原图形中,连结后得到原图形,然后利用梯形面积公式求解.
解答: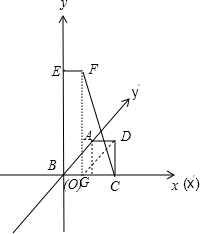 解:如图,
解:如图,
直观图四边形的边BC在x′ 轴上,在原坐标系下在x轴上,长度不变,
点A在y′ 轴上,在原图形中在y轴上,且BE长度为AB长的2倍,过E作EF∥x轴,
且使EF长度等于AD,则点F为点D在原图形中对应的点.
∴四边形EBCF为四边形ABCD的原图形.
在直角梯形ABCD中,由AB=2,AD=1,得BC=
+1.
∴四边形EBCF的面积S=
(EF+BC)•BE=
(1+
+1)×4=4+2
.
故选:B.
 解:如图,
解:如图,直观图四边形的边BC在x′ 轴上,在原坐标系下在x轴上,长度不变,
点A在y′ 轴上,在原图形中在y轴上,且BE长度为AB长的2倍,过E作EF∥x轴,
且使EF长度等于AD,则点F为点D在原图形中对应的点.
∴四边形EBCF为四边形ABCD的原图形.
在直角梯形ABCD中,由AB=2,AD=1,得BC=
| 2 |
∴四边形EBCF的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故选:B.
点评:本题考查了水平放置的平面图形的直观图的画法,考查了原图形和直观图面积之间的关系,最好记住结论:
=2
,该题是基础题.
| S原 |
| S直 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图),∠ABC=45°,AB=AD=1,DC⊥BC,则这块菜地的面积为
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图),∠ABC=45°,AB=AD=1,DC⊥BC,则这块菜地的面积为 有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示),则这块菜地的面积为
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示),则这块菜地的面积为