Question

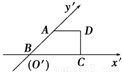
有一块多边形的菜地，它的水平放置的平面图形的斜二测直观图是直角梯形（如图），∠ABC=45°，AB=AD=1，DC⊥BC，则这块菜地的面积为

2+

2

2

．

Answer 1

分析：求出直观图中，DC，BC，S_梯形ABCD，然后利与用平面图形与直观图形面积的比是2

2

，求出平面图形的面积．

解答：解：DC=ABsin 45°=

2

2

，BC=ABsin 45°+AD=

2

2

+1，
S_梯形ABCD=

1

2

（AD+BC）DC=

1

2

（2+

2

2

）

2

2

=

2

2

+

1

4

，
S=

4

2

S_梯形ABCD=2+

2

2

．
故答案为：2+

2

2

点评：本题考查斜二测画法，直观图与平面图形的面积的比例关系的应用，考查计算能力．