题目内容
函数 的零点一定位于的区间是 ( )
的零点一定位于的区间是 ( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
C
解析试题分析:将1,2,3分别代入计算,可得 根据函数的零点存在定理可知,该函数的零点一定在区间(2,3)内.
根据函数的零点存在定理可知,该函数的零点一定在区间(2,3)内.
考点:本小题主要考查函数的零点存在定理的应用.
点评:利用函数的零点存在定理时只要将各端点分别代入函数式,判断符号即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若函数f (x) = x
 在[1,+∞)上是增函数,则实数p的取值范围是( )
在[1,+∞)上是增函数,则实数p的取值范围是( )
A. | B. | C. | D. |
下列各组函数中表示同一函数的是 ( )
A.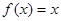 与 与 |
B. 与 与 |
C. 与 与 |
D. 与 与 |
下列函数中,既是偶函数,又在区间 上单调递减的是( )
上单调递减的是( )
A. | B. | C.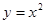 | D. |
函数 ( )
( )
A. | B. | C. | D. |
定义域为R的函数 的值域为
的值域为 ,则函数
,则函数 的值域为
的值域为
A. | B.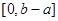 | C. | D. |
若 ,则函数
,则函数 的解集是( )
的解集是( )
A. | B. |
C. | D. |
已知函数f(x)是R上的增函数,A(0,-2),B(3,2)是其图象上的两点,那么|f(x+1)|<2的解集是( )
| A.(1,4) | B.(-1,2) |
| C.(-∞,1)∪[4,+∞) | D.(-∞,-1)∪[2,+∞) |
下列函数中,以 为最小正周期的偶函数是( )
为最小正周期的偶函数是( )
A. | B. |
C. | D. |