Question

【题目】已知函数，为偶函数，且当时，．记．给出下列关于函数的说法：①当时，；②函数为奇函数；③函数在上为增函数；④函数的最小值为，无最大值． 其中正确的是________．

Answer 1

【答案】①③④

【解析】

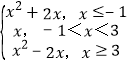g（x）=，F（x）=max{f（x），g（x）}（x∈R）=．画出图象，数形结合即可得出．

g（x）=，

F（x）=max{f（x），g（x）}（x∈R）=．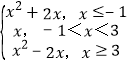

画出图象，

由图象可得：①当x≥3时，∵x2﹣2x≥x，∴F（x）=x2﹣2x，因此正确．

②由图象可得：函数F（x）不为奇函数，因此不正确．

③﹣1≤x≤1时，x＞x2﹣2x，可得函数F（x）=x，因此函数F（x）在[﹣1，1]上为增函数，正确．

④x≤﹣1时，g（x）=x2+2x≥x，可得F（x）=x2+2x≥﹣1，综上①③④可得：函数F（x）的最小值为﹣1，无最大值，正确．

其中正确的是 ①③④．

故答案为：①③④．